Main Page/PHYS 3220/Coupled Motion
Contents
Coupled Oscillatory and Rotational Motion
Abstract
In this experiment a magnetically levitating motion device is used to study coupled oscillatory motion, as well as coupled rotational-oscillatory motion. Beat patterns can be observed over long periods of time due to the low friction. Computer-interfaced data acquisition allows one to perform a Fourier analysis of the motion.
Introduction
Coupled Oscillators
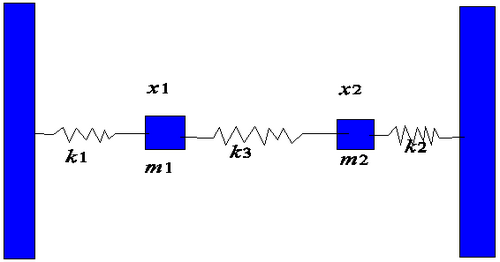
The problem of two coupled harmonic oscillators represents a textbook example that is amenable to a closed-form solution (see references or other texts on Classical Mechanics). The most striking feature that can be observed in coupled pendula with masses m1 and m2 is the beat pattern: if one, e.g., m1 is initially at rest, while m2 is struck, an oscillation starts in m2, but is then transferred into m1 and back. This oscillation of the amount of kinetic energy in each of the oscillators goes on forever.
|
|
A Maple worksheet is provided that generates the solution for the two normal modes of the problem of two masses connected by three springs. A superposition of the normal modes displays the beat pattern. For closely spaced frequencies of the normal modes (the spring constant k3 for the spring connecting the two masses being much weaker than k1 and k2) the beat pattern is particularly impressive.
Resonant motion
A mechanical system in real life is always damped. The investigation of a driven damped harmonic oscillator shows that the introduction of a small amount of friction has some influence on the resonance behaviour. Suppose that a periodic driving force with circular frequency ω excites an undamped harmonic oscillator with natural circular frequency ω0 (ω02=k/m). According to the mathematical solution the system will be driven to larger and larger amplitudes as time progresses. The introduction of damping changes this behaviour qualitatively. The natural frequency increases slightly with the damping (ω0'), but more importantly the asymptotic behaviour in time changes: a constant-amplitude oscillatory motion with frequency ω results. The magnitude of this amplitude depends on the resonance condition: for ω=ω0' it acquires a maximum. The periodically driven harmonic oscillator is obviously relevant for the problem of coupled motion: one can consider the motion of one mass as driving the other and vice versa.
Fourier analysis
A useful mathematical tool to investigate the motion of real-life objects is Fourier analysis. It can be used for strictly periodic functions on some interval (Fourier series) and for non-periodic functions (Fourier series), which can be considered as the limit of the former when the periodicity interval T is extended to infinity (cf.. ref. 7). The advantage of Fourier analysis lies in the fact that a seemingly complicated signal in the time domain can be composed of a superposition of a few oscillations with different frequencies and amplitudes and phases. In the case of discretely sampled time series the continuous Fourier transform (FT) is replaced by a discrete FT, which can be calculated very quickly on a computer (fast FT, or FFT; cf. ref. 8).
To analyze the data in this experiment you are not required to understand the mathematical details of Fourier analysis. However, a good understanding of the usefulness and pitfalls of discrete FTs belongs to the repertoire of a seasoned physicist, since it applies to many areas of physics, and experimental physics in particular. The data acquisition program will perform the FFT for you. You are only required to understand these data properly. A periodic signal will show in the frequency domain as a sharp line. The truncation of the signal to a finite length (finite wave train) introduces a broadening around the central frequency. Similarly a beat pattern should show theoretically a sum of two spikes (located at the two frequencies corresponding to the normal modes). In practice one cannot record an infinitely long signal, and therefore a broadening arises in the FT.
Procedure
Familiarize yourself with the so-called 'frictionless' rotational-vibrational motion device. Be careful when spinning the `bone' not to jerk it out of the suspension. Dropping it to the floor can easily destroy it. Understand how two permanent magnets in the base together with two magnets in the bone and the glass plate at one end generate a potential well. Ignore rotational motion until the last part of the experiment. The oscillatory motion can be decomposed into two fundamental modes: a perfect vertical oscillation, as well as a horizontal mode. The horizontal mode couples necessarily to the vertical motion, since there is a variation in the combined gravitational and magnetic fields as the end of the bone moves sideways.
The computerized data acquisition system uses electromagnetic induction to convert the oscillatory motion of the magnet inside the bone into an electric voltage that is amplified by an operational amplifier (OpAmp) and passed into a computer interface that converts the analog signal into a digital signal (ADC: analog-digital converter). The signal range accepted by the ADC is 0-5V, and thus the OpAmp circuit has to shift the AC signal generated by the induction coil to a non-zero offset. This offset should be subtracted before a FT is performed, since it represents an artificial DC bias (zero-frequency component).
Recording the Data
Connect the AC adapter to power up the Serial Interface Box (SIB). Connect the magnetic coil with its amplifier (powered by the SIB) to input 1 using the DIN (5-pin) plug. Verify that the SIB is connected to the computer through a serial cable. Turn on the computer.
The software is located in the directory c:\LOGGER.
At the c:\ prompt, type C:\win.
Then press the Enter key.
An important selection concerns the data acquisition rate, i.e., how many samples are taken per time interval. This is achieved by stepping from the Main menu (right mouse button) to the Collect selection, and Data Rate subselection. Noting that the frequency of oscillation is in the few-Hertz range we find that we can choose either the maximum rate for the SIB (50 Hz), or one-half that value. The latter will permit the program to record longer sequences (and keep them in memory). Note that there will be a trade-off: long sequences allow to record with a good frequency resolution; a high data acquisition rate allows having a high value for the maximum frequency to be detected. This is a characteristic of any discrete data sampling procedure.
Familiarize yourself with the procedures to adjust the scales (double-click while pointing to the graph to bring up an intuitive interface). Note that you have two data channels (inputs) that are recorded as a function of time, designated as P1 and P2 representing port 1 and port 2. You have many choices, one can graph either of them as a function of time (or even P1 vs P2 in which case time appears as a parameter - this permits to use the SIB to determine functional relationships where time is only used as an auxiliary variable). Besides showing the original data it is possible to perform a FFT. From the main menu it is obvious how to set up multiple windows, analyze the data with a pointing tool (to read off numerical values), etc.
It is possible to export data to ASCII files for further processing with a Spreadsheet or graphing program. One can record sessions, and load session files with preset options for the windows, data acquisition rate, time interval, etc.
- Record purely vertical motion and determine its natural frequency.
Place an induction coil vertically above the swinging end of the bone. You should find a good height to obtain a strong signal; however, being too close results in the bone clinging to the iron core of the recycled relay coil. Gently tap the bone to put it into a perfect vertical motion and record the signal. Observe over what time scale the motion damps out.
Estimate the natural frequency for this mode from the data in the time domain. Perform a FFT and report your findings. Compare your recorded data series to the known solution of the damped harmonic oscillator. What is the value of the friction constant γ?
- Observation of beat patterns.
Mount a second induction coil to pick up the horizontal motion. Use the coil that can be disconnected from the OpAmp. Gently tap the end of the bone in the horizontal direction. Can you see a beat pattern with your eyes? Record on both data channels simultaneously and observe the beats while data are acquired. What are your findings from the FFT? What does the beat pattern imply for the separation of the two basic modes? Are there additional structures in the FFT spectrum? Note that the device is nonlinear in the sense that the harmonic oscillator approximation is at best valid for small-amplitude oscillations (cd. the pendulum).
- Resonant excitation.
Disconnect the horizontal coil from the OpAmp and connect it to a function generator. Feed a sinusoidal signal into the coil from a function generator. Scan the 1-10Hz interval and explore for what frequency range larger amplitudes are observed. Why does a beat pattern occur?
- Rotational-vibrational motion.
Keep the pick-up coil for the vertical motion. Connect the photodetector to the other port and position it such that it is observing the bone. Illuminate the observed section of the bone with a lamp, such that the photodetector picks up the stroboscopic reflections. Note that the red-green contrast is picked up very well by the phototransistor due to its increased sensitivity in the red/infrared regime. Learn how to put the bone into a smooth rotation without vibrations with speeds exceeding 5 revolutions per second. Watch what happens as the rotation slows down. Record time series for the rotation and vibration and observe the regime when the motion becomes interesting. Explain your observations.
References
- Arya, A. P., Introduction to Classical Mechanics, (1990).
- Fowles, G., Analytical Mechanics, (Saunders).
- Goldstein, H., Classical Mechanics, (Addison-Wesley).
- Klepper and Kolenkow, An Introduction to Mechanics.
- Symon, K., Mechanics, (Addison-Wesley).
- Spiegel, M., Theoretical Mechanics, Schaum's Outline Series (Mc-Graw-Hill).
- Arfken, G.A., Mathematical Methods for Physicists, (Academic Press).
- A.P. French, Vibration and Waves (W.W. Norton, 1966).