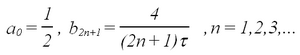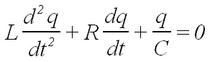Main Page/PHYS 3220/Digital Oscilloscope
Contents
Digital Storage Oscilloscope
In this experiment we use a function generator to produce rectangular pulses which are recorded and analyzed using a modern digital storage oscilloscope capable of performing a fast fourier transform (FFT) on a given signal. Then the behaviour of a simple RC (integrator) circuit fed by a square wave pulse is analyzed both in the steady-state and transient (turn-on) regimes. Finally the square-wave pulse is used to induce damped harmonic motion in an LC circuit.
Introduction
The behaviour of short time-varying signals can be investigated easily with a digital storage oscilloscope (DSO) that will allow you to trigger single events and to store them for any length of time. Periodic signals play an important role in many areas of physics. Periodic signals are conveniently analyzed in terms of harmonic (or frequency) content, either by means of a Fourier series or by a Fourier transform [1]. Typically, oscilloscopes display signals in the time domain. The DSO you are using here will allow you to process these signals so they can be displayed in the frequency domain by using an FFT signal processing module included in the DSO. For a finite wavetrain recorded at discrete time intervals two parameters impose practical limitations on acquiring knowledge about the frequency content of a pulse. The sampling rate Δt limits the maximum frequency that can be recorded (intuitively: a signal that changes sign at every tj = j Δt has the highest frequency that can be represented on the discrete time axis). The length of the recorded signal, T, limits the frequency resolution, Δf: the lowest frequency that can be recorded corresponds to a wave with a period that equals T.
Thus, the Fourier transform that would be available in an ideal measurement (continuous sampling and infinite length of measurement)
| (1) |
this is replaced by a discrete Fourier transform:
| (2) |
where the length of the signal in the time domain is given by T = N Δt , the maximum frequency (called the Nyquist frequency) is actually one-half of the inverse sampling rate fc = 1/(2 Δt) as the range of frequencies ranges in principle from -fc to fc (but the answer is symmetric in f so we are only interested in the range [0, fc]). The frequency resolution equals Δf = 1/(N Δt). There are numerous problems associated with the replacement of eq (1) by eq (2), these problems are discussed in detail in [2] (and hinted at in the manual for the Tektronix TBS 1052B-EDU oscilloscope). To minimize some of the errors one usually multiplies the time signal with a window function whose main purpose is to provide a smooth switching of the pulse and thereby to eliminate artificial high-frequency components that would be associated with chopping a periodic signal at t = 0 and t = T and assuming periodicity (wrap-around).
In a digital storage oscilloscope (as in computer programs that analyze recorded data) an FT function is provided by an efficient algorithm (fast FT = FFT) [2]. In a computer interfaced experiment one usually chooses the sampling rate and temporal record length freely. However, with the DSO these parameters are not independent and are actually controlled simultaneously by the DSO time base control. Furthermore, the number of points used in memory (for display on the screen and transfer to a computer) for a single trace is fixed. The FFT algorithm requires this number to be a power of 2 (typical numbers are 1024, 2048, etc. ).
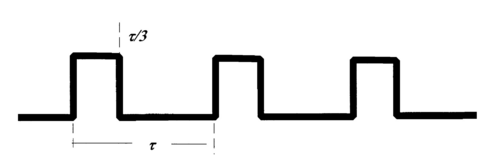
Consider a rectangular pulse, and a square-wave in particular. It can be thought of as a superposition of a sine wave with the same period τ, given by admixtures of sine waves with higher frequencies (or periods that are simple fractions of τ). This is known from Fourier series expansions of this periodic function. Only sine waves with odd multiples of the base frequency contribute (odd-order harmonics), and the coefficients in the linear combination can be calculated [1]. In part 1 of the experiment the Fourier spectrum (which could detect any frequency components, and not just multiples of the base frequency) is taken for rectangular pulses with different duty cycles. The objective is to show that for a pulse with duty cycle (τ/n)/τ = 1:n (cf.. Fig. 1) the nth harmonic is absent. For a square-wave pulse (1:2) only odd orders appear.
|
Figure 1 - A rectangular pulse with a duty cycle of 1:3.
|
For a square wave pulse the harmonic coefficients can be calculated from the Fourier series expansion to be (we assume a signal that ranges between 0 and 1)
| (3) |
Procedure
Part 1: Harmonic Analysis of Rectangular Pulses
The Tektronix TBS 1052B-EDU Oscilloscope
Connect the 50 Ω output of the function generator (WAVETEK, model 184) to Ch.1 of the DSO. Turn on the power switch of the function generator and familiarize yourself with the effect of varying the frequency settings of the function generator, and learn how to use the digital scope. Links to the user manuals: DSO User Manual and Wavetek FG User Manual. Refer to section 3 of the WAVETEK instruction manual for a description of the function generator operation controls. There are several menus that control the DSO operation. For this part you need to use the menu that controls the first Y channel (CH 1), and possibly the TRIGGER menu. In the TRIGGER menu it is important that the Source of triggering be specified as CH 1 and the Mode of triggering be set on Auto. (Only for the measurement of the transient behaviour of an RC circuit will you need to switch to Single Mode). The 5 buttons to the right of the LCD display are used to toggle through the options indicated on the DSO screen.
The display of channel 1 or 2 can be turned on and off using the CH1 and CH2 menu buttons. Once the menu for a given channel is activated the 5 buttons to the right of the LCD display can be used to control:
- the Coupling (DC, AC, Ground).
- Bandwidth limit (suppress high frequencies if desired).
- Volts/Division: coarse or fine (this controls whether the knobs carry out the usual large incremental voltage scale steps (1V, 2V, 5V, etc. ) or fine steps that actually simulate an infinitely variable scale control on an analogue scope).
- Probe (10X if the Tektronix probe is attached, 1X if a simple coaxial cable is used (this setting alters the display of scale for Volts/Division being measured - it is needed as the supplied probes step down the voltage by a 1:10 ratio, i.e., 1 V applied to the probe results in 0.1 V at the coaxial input to the scope).
- Invert (on/off). When “on” this will invert the displayed signal.
The MEASURE menu can be used to find period and frequency of a periodic signal, in this case a pulse. a) The top button controls whether the lower 4 (of the 5 to the right of the LCD) provide control over the source or the type of measurement. Sources can be CH1 or CH2; Types of measurement are: Frequency, Period, Mean (average voltage), Peak-to-peak voltage, Cyc RMS(?), Rise and Fall times for a pulse, as well as positive and negative width (this is particularly useful for a rectangular wave form).
The CURSOR menu will give you control over the position of a set either of two vertical or two horizontal cursors that span the display area. These are controlled by the multipurpose knob and selected using the lower two buttons to the right of the LCD screen. A useful feature of the cursors is that one can read off the cursor positions indicated on the right of the screen as digital numbers, for the horizontal positions the difference indicates a time with likewise a vertical difference indicates signal amplititude its inverse (as frequency).
The MATH menu is invoked by pressing the red button labelled M to the left of CH 1. In math mode one can add, subtract or multiply CH 1 and CH 2 signals.
The FFT menu is invoked by pressing the yellow button labelled FFT located just below the math menu button. With it on can carry out a Fourier transform FFT of CH 1 or CH 2 separately; within the FFT menu one can choose a windowing function [Rectangular implies no windowing, Hanning [2] a standard function that compromises between accurate measurement of frequency amplitudes and the accuracy of frequency measurements (the windowing function introduces an artificial width: a single-frequency signal is broadened in frequency content), Flattop provides more accurate amplitudes in the Fourier spectrum. Finally one can zoom in on the FFT spectrum, since the display actually only uses a few hundred pixels in the horizontal (and vertical) directions, whereas an FFT is calculated with over 4000 points. Note that the FFT is calculated for incoming data, i.e., it is not possible on the TBS 1052B-EDU to record a pulse and then carry out the FFT for that pulse.
The vertical scale used for the FFT is calibrated in decibels. The logarithmic decibel scale is explained in 1st year physics texts in the context of sound waves. It is a relative scale, i.e., it depends on some reference strength (which in the case of the TBS 1052B-EDU is chosen to be: 0 dB = 1 V RMS amplitude). A drop by 3 dB corresponds approximately to a reduction by a factor of 2 in amplitude.
With the RUN/STOP button (top right on the scope) you can capture the display (helpful if the signal is shaky), the HARDCOPY button provides a screenshot output to a printer connected to the parallel port, while AUTOSET helps to find settings for some acceptable screen display if you have no idea how to set the vertical amplification and the timebase (horizontal) for your particular signal. It is customary to start by pressing autoset, observe the settings chosen by the scope, and subsequently fine tune the settings as appropriate.
Measurement of the rectangular pulses produced by the function generator outputs
Begin detailed measurements by setting a (1:n) duty cycle at some frequency with the function generator. Carry out the harmonic analysis using the FFT menu functions. Save the data of the time signal and the FFT using a USB stick to include with your report. Provide your observations about the harmonic spectrum.
Measure rise and fall times for the square wave pulse. For this purpose start with a display of a few cycles on the screen. Now move one of the edges (first a rising, later a falling edge) to the center of the display. Turn the (horizontal) timebase switch to display shorter segments of the pulse until the initially vertical line acquires the characteristic shape for a charging capacitor (discharging in the case of a falling edge), i.e., it becomes an exponential function. Note the time scale at which this happens. Use the Measure menu to obtain a measurement of the rise and fall times (it will depend somewhat on the segment displayed on the screen, since it measures between 90 and 10 % of the signal displayed; cf. the manual for the TBS 1052B-EDU). You should spend some time thinking about clocks used in computers, how fast they have to be (PC chips run internally at speeds in the low GHz range these days, while the entire computer (the bus) can be clocked at up to 66 MHz), and how the rise and fall times are important since during those times the logical state (0 or 1) is really undetermined. There can be no ‘perfect’ square-wave or rectangular pulse.
In the following exercise observe how a simple logic gate can be used to shape the pulse. Use the TTL output of the function generator on Ch. 2 and look at the same characteristics as with the 50 Ohm output. Compare the measured rise and fall times of the two outputs. You can overlap the two signals and zoom in to observe the two signals in detail.
To deepen your understanding of the idea of triggering on a signal it is interesting to display the signals from two uncorrelated generators: use the signal from the one of the function generator output (50 Ohm output or TTL output) on one channel and connect the internal 1 kHz generator to the other. (See TBS 1052B-EDU scope diagram – probe compensation terminal lugs located in the DSO manual.) From the TRIGGER menu choose to trigger on either CH1 or CH2. What do you observe? Use the RUN/STOP button repeatedly to capture still images and explain the behaviour.
Part 2: Charging and Discharging a Capacitor
Set the TTL output of the function generator to produce a square-wave signal of a given frequency (rectangular pulse with duty cycle 1:2). Connect an RC circuit such that the capacitor C is charged via the variable resistor box R. Measure the voltage as produced by the function generator (use a BNC Tee to split the TTL output) on CH1 and the voltage across C on CH2. Note that CH1 and CH2 have a common ground: think before making the connections. The physics of charging and discharging a capacitor is explained in first-year physics texts. Familiarize yourself with the material, we provide no equations here. You need to realize that during the ‘low’ output the square-wave generator acts as a short, i.e., it discharges the capacitor through the resistor R (the internal resistance of the function generator is often in the 50 Ohms range which is negligible if R is in the kΩ range).
For a fixed choice of R and C (calculate the time constant T) make measurements for three different settings of the square-wave frequency. Adjust the period τ (to have a 1:2 duty cycle) such that the three cases cover a period τ less than T, comparable to T, and bigger than T. Use DC coupling on both channels, and observe the steady-state behaviour of the sequence of periodically charging and discharging. Provide explanations to compare the three cases. Why is the voltage across the capacitor periodic? In the next section you will measure the transient or turn-on behaviour. Fig. 3 is provided as an illustration of the case where τ < T such that the capacitor does not fully charge or discharge during one of the half-periods τ/2. Each segment of the curve is obtained from the solution to the differential equation describing the charge or discharge regimes, and the correct initial condition is being applied (we assume no charges on the capacitor plates at t=0).
|
Figure 3 - RC circuit response to a periodic signal.
|
An interesting quantity to measure in the charging/discharging RC circuit is the voltage across the resistor, which according to Ohm’s law provides a measure of the current in the circuit. Thus, it is possible to observe how the current changes sign and jumps from some low (possibly near-zero) value at the end of a cycle to ±U/R. Mathematically the answer is discontinuous, and this is interesting to investigate in real life. From a measurement point of view the matter can be straightforward: if one uses an external function generator, one can simply connect a probe across R. Note, however, that one cannot also connect the other probe across the capacitor (or to measure the signal coming from the function generator), since CH1 and CH2 have a common ground (and the internal 1 kHz generator uses this ground as well). One trick, however, is to perform the same measurement as before on CH1 and CH2, and to display the difference between the two channels. This is done by using the CH1 + CH2 option on the MATH menu while inverting one of the channels. Perform such a measurement with several cycles shown on the display. There is an apparent discontinuity in the voltage across R (obtained as the difference between the voltage produced by the function generator and the voltage across C). While a discontinuity is located at the center of the screen zoom in using the TIMEBASE adjustment. At what times scale do you resolve the discontinuity, and why?
Part 3: Transient Behaviour (cf.. Fig. 3)
Use the same connections as in Part 2, i.e., consider the charging and discharging of a capacitor C through a resistor R. In this part we are interested in the first 10-20 cycles of a square-wave pulse to see how the RC circuit approaches its nearly-periodic behaviour observed in the previous part. For this purpose one has to set the triggering onto the mode single pulses and then adjust the trigger level for a small positive voltage. The RUN/STOP button is used to acquire the signal. The trigger level is set to such a value that when the square-wave generator is disconnected, the scope indicates readiness to record but is not triggered. As the square wave is applied by flipping a switch a single trace is recorded. It is possible to adjust the timing of the single trace with the horizontal adjustment, and by repeating the measurement.
Make observations for a settings of the square-wave time constants τ < T, and comment on your results. Why is the other limit τ < T uninteresting?
Part 4: Damped Oscillations in an LC circuit
Here we use square-wave pulses to induce damped oscillations in a circuit that consists of an inductance L and a capacitance C connected in series. Consult a first-year physics text (e.g., [4]) on the physics of storing electrical energy in the form of an electric field in C and in the form of a magnetic field in L, and how they are exchanged in an RLC circuit. Note that a resistance is present even if no resistor is put into the circuit, as there is no ideal coil, i.e., it always has an Ohmic resistance. The differential equation that can be derived from Kirchoff’s law together with the properties of a capacitor, an inductance and a resistor is comparable to that of a damped harmonic oscillator. For the capacitor charge q(t) we obtain:
| (4) |
Here L plays the role of inertia (mass), R appears as a friction constant, and the capacitance C plays the role of the spring constant. Understand why the application of a square-wave pulse corresponds to kicking a damped harmonic oscillator: q(0) = 0, q’(0) ≠ 0.
In the case of weak damping (undercritical damping) the solution to eq. (3) has the form:
| (5) |
Record time signals for an LC circuit with known capacitance and inductance, and compare with the solution to the differential equation. Is the measured frequency consistent with the solution? Estimate the resistance from the decrease in the envelope. You can measure the resistance R with a digital voltmeter. Note, the commercial function generator has a typical internal resistance of 50 Ω. Perform measurements with a variable resistor box R included in the circuit and adjust R to find critical damping (in addition to the undercritically damped situation described above). Critical damping is obtained when the time constant of the damping T = 2L/R equals the inverse of the natural (circular) frequency ω.
References
- G.A. Arfken, Mathematical Methods for Physicists, Academic Press.
- W.P. Press, S. Teukolsky, Vetterling, Flannery, Numerical Recipes, Chapter 12, Cambridge University Press.
- Horowitz Hill, The Art of Electronics, chapter 5.14, Cambridge University Press.
- R. Wolfson, J.M. Pasachoff, Physics, 2nd ed., chapter 33-3, Harper Collins, New York 1995.