Main Page/PHYS 3220/High-TC Superconductivity
Contents
High-TC Superconductivity
Introduction
The discovery of high-temperature superconductivity in 1987 has made it possible to study the change in conductivity at temperatures above the boiling point of liquid nitrogen (77 ○K). Many ‘normal’ metals (e.g. Pb, Hg) undergo a phase transition at a few ○K to a state where the conduction of electricity is effected by correlated electrons (Cooper pairs) and is almost resistance-free. High-temperature superconductivity on the other hand occurs in complicated compounds, e.g., yttrium barium copper oxide that usually exhibit conduction in two-dimensional planes of the crystal. The conduction mechanisms are not well known yet, but it is clear that the usual theory of superconductivity (BCS model) is not applicable. Also the change in conductivity is not as drastic as in a conventional superconductor.
In this experiment we investigate a semiconductor chip made of Y1Ba2Cu3O7 that contains a pair of Josephson Junctions (JJ). The combination of two JJ in parallel is called a SQUID - a superconducting quantum interference device. It permits to display quantum phenomena on a macroscopic scale, which is very remarkable, since usually quantum phenomena are restricted to the microscopic scale. The SQUID can also be used as a simple probe that goes into a superconducting state when T < Tc , provided that the current passed through it is not too large.
The experiment contains three parts: (i) a measurement of the current-voltage characteristic for the JJ connected in parallel as the chip is immersed in liquid nitrogen; (ii) a measurement of the resistivity of the JJ as a function of temperature; (iii) a measurement of the response of the JJ to a magnetic field induced by a coil that is imprinted on the circuit board. The latter experiment demonstrates the quantization of magnetic flux in a JJ loop.
All three experiments are relatively straightforward to perform, but the analysis of part (iii) requires a significant amount of literature survey (see ref. 1, chapter V, and the references cited there) to understand the physics.
Procedure
The equipment consists of the SQUID chip mounted on a rod with a metal shield to reduce the effects of external magnetic fields, a control box that contains circuitry to supply voltages and to amplify voltages in the microvolt range to millivolts that can be displayed on an oscilloscope. For the liquid-nitrogen bath a one-litre dewar bottle is used, and a temperature gauge is assembled using a silicon diode, a constant-current power supply and a digital voltmeter.
CAUTION: The handling of liquid nitrogen requires special care: safety glasses and gloves are required for filling and carrying the dewar flask, immersion of objects into the liquid nitrogen is accompanied by boiling and spray of the fluid that will cause severe burns if it comes in contact with your skin or eyes! Wear glasses and appropriate clothing and make sure not to trip over the dewar flask while experimenting!
The procedure is not described in detail here, use the appropriate sections of ref. 1.
Part 1
The current-voltage characteristic is taken in order to demonstrate superconductivity and to understand that the superconducting effect is possible only up to a certain critical value of the current. An overview of the experiment setup is given in section 2.2 of the Mr. SQUID User Guide [1]. Be sure to perform the battery check and turn the device off when not in use (so as not to deplete the two 9V batteries at a fast rate). Connect the oscilloscope that is operated in X-Y mode. The control box has to be operated in V-I mode for parts 1 and 2 of the laboratory.
The following remarks are important to understand the results displayed on the oscilloscope. An oscilloscope displays voltages, and contains amplifiers for both X and Y (we are not using the timebase at all for these measurements) to boost signals from the millivolt range to create deflections of the electron beam in the tube. To display a current one needs to pass the latter through a resistor to measure the voltage that arises. This resistor is part of the control box and has a value of 10 k Ω. Thus, one converts the X display (Vx in millivolts) to a current by dividing by 10 k Ω (Ohm’s law). For the Y display another conversion is required. The voltage measured across the JJ is in the microvolt range. To display it on a scope an amplifier is contained in the control box that boosts it to the millivolt range, i.e., on the Y channel we observe Vy in millivolts. The control box amplifier for the Y channel has a gain of 10,000. This value was chosen such that the resistance (in Ω) can be read off directly from the ratio Vy/Vx as observed on the scope (Ohm’s law for the JJ in the regular or superconducting regimes). When quoting values for the critical current or voltages make sure to perform a proper conversion to true values!
Follow the procedure outlined in Sections 3.1 -to- 3.5 of ref. 1 to obtain a display of the V-I characteristic on the scope (Fig. 3.3 on p. 12). Adjust the flux bias control to optimize the superconducting regime. This control regulates how much current is passed through the gold coil imprinted on the circuit board (see Fig. 3.6 on p. 20) and helps to cancel magnetic fields trapped in the SQUID while it was cooled to below-critical temperatures.
Fig. 3.5 on p. 14 explains how to read off the critical current (displayed as Vx) and the resistance in the non-superconducting regime (super-critical current). A factor-of-two correction for the resistance and the critical current comes from the fact that two JJ are connected in parallel. The critical current (magnitude) is given by dividing the horizontal width of the flat region of the V-I characteristic in addition by two, since the positive and negative current directions are displayed. The two parallel JJ are assumed to be identical (which is not quite true in practice). Try to determine the resistance in the superconducting regime by increasing the Y-magnification on the scope.
Calculate the critical current Ic and the normal resistance RN. The product of these two quantities determines a voltage that characterizes the SQUID and enters the beta parameter to be determined in part 3. Use the provided data sheet to report your values. Once you have read off the critical current and the normal resistance you can lift the SQUID carefully out of the dewar and observe on the scope how the V-I characteristic changes as the JJ warm up.
Do not touch any parts lifted out of the dewar until they have warmed to room temperature (it burns)! Wear safety glasses and gloves.
Part 2
A temperature gauge can be readily built using a silicone diode as a probe. The resistance of the diode under forward bias is controlled by the temperature as the number of charge carriers (holes in the p-region, electrons in the n-region) is a direct function of T. The details are given on pp. 78-79 of ref. 1, or in ref. 2.
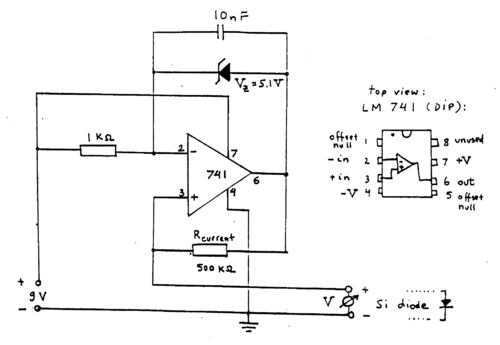
To measure the resistance of the Si diode a constant-current power supply in the microampere range is required (Fig. 1 below). This is achieved using an operational amplifier (OpAmp) that compares a reference voltage obtained from a Zener diode with the voltage generated across a resistor (Rcurrent) by the current load. The OpAmp supplies more or less voltage such that the difference between its + and - inputs balances to zero.
|
Figure 1 -Constant-current supply for the Si diode temperature gauge.
|
Use Fig. 1 to carefully assemble the circuit on a breadboard. After connecting the Si diode with the appropriate polarity for forward biasing a reading of about 0.36 Volts should occur at room temperature. For full immersion into the liquid nitrogen bath the voltage reading will be about 0.76 Volts. The Si diode is taped to the back of the SQUID chip at the appropriate height. Temperatures above 77 K are obtained by holding the SQUID probe at a fixed height above the liquid nitrogen level. The resistance is measured by reading the slope of the V-I characteristic (keep the settings of Part 1 of the experiment, and make sure to display the middle portion of the V-I characteristic. Perform the measurement as outlined in Section 7.1 of ref. 1, pp. 55-61.
Part 3
Perform the measurement of the voltage vs. magnetic flux V-Φ characteristic as described in sections 3.6 -to- 3.8 of ref. 1. Make sure to calculate the current ΔI and the modulation voltage ΔV correctly from the voltages Vx and Vyrespectively.
Calculate the βL parameter for the given SQUID chip using eqns 3.1 and 3.2 from p. 24 respectively and compare where it falls on Fig. 3.9 (ref. 1, p. 20).
Questions
- Estimate your errors while reading the oscilloscope and quote results with estimated errors.
- For part 1 explain in detail the shape of the V-I characteristic.
- For part 2 extract your estimate of the critical temperature Tc and compare with the expected result. How is Tc approached from above? Discuss sources of error in the measurement.
- Provide a calibration curve for the temperature gauge assuming a linear relationship between the voltage across the diode and temperature. Can you take a control reading at a third temperature value to check the linearity?
- For part 3 provide a detailed explanation of the V-Φ characteristic (use Fig. 5.8, p. 35 of ref. 1).
- Provide sketches of the oscilloscope displays (use tracing paper) and record the X- and Y-amplifier oscilloscope settings for each for the measurements in parts 1 and 3.
References
- R.W. Simon, M.J. Burns, M.S. Colclough, G. Zaharchuk, and R. Cantor (STAR Cryoelectronics, LLC.), Mr. SQUID: User’s Guide ,2007.
- C. Kittel, Solid State Physics.
- A. Beiser, Concepts of Modern Physics.
- P. Schmuser, Superconductivity, Lecture Notes.