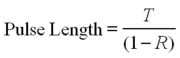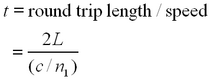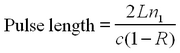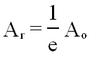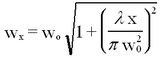Main Page/PHYS 4210/He-Ne Lasers
Contents
He-Ne Lasers
In this experiment we first align an open-ended laser. Then we set up some transverse mode patterns, and perform further exercises and experiments to understand how a laser works.
Key Concepts
|
|
Reading and Exercises
- Read pages 94 to 105 and pages 100 to 112 from Preston-Dietz, available here[1].
- Carry out Exercise 1 (pg. 100), Exercise 2 (pg. 103), Exercise 3 (pg. 104), and Exercise 4 (pg. 104).
- Complete Exercise 1 (pp 111-112). Do not forget to answer the last question of the exercise: Calculate the frequency difference between two adjacent axial modes TEMoom & TEMoo(m+1).
- Submit all exercises as part of your report, either in the introduction or as an appendix as you deem appropriate.
Experiments
Aligning the laser
Align the laser until it begins lasing. The TA will discuss techniques to accomplish this.
When you are successful with the aligning process, and lasing is achieved, try varying the distances between the mirrors (using the adjusting screws on the laser mount) that still supports lasing. Record, in your lab book, the aligning process used, maximum, minimum and 'best' distances between the mirrors.
What the radius of curvature of the mirrors which form the optical cavity?
Use the polarizers to determine the polarization of laser.
Assume that the He-Ne produces 3 mW of laser output power and that the electrical data given applies to your gas discharge tube. Compute the efficiency, in percent, for converting electrical energy to red laser light energy with this He-Ne laser. Discuss your results.
Brewster's Angle
Using the glass plate provided, find an approximate value for the Brewster's angle. You can determine this by rotating the glass plate until lasing stops. Only at the Brewster's angle does lasing resume.
Knowing that the tangent of the Brewster's angle is the ratio of the refractive indices of the lasing medium to air, determine the refractive index of the glass medium.
Every resonant laser cavity has a characteristic quality factor or Q that measures the internal losses. The higher the Q, the lower the losses.
A Q-switch pulse can be made by blocking one end of the mirror, then exciting the medium and then quickly unblocking the mirror. Stimulated emission will quickly drain the stored laser energy from the cavity in a short pulse with peak power much higher than the laser can produce. One can think of a Q-switch as a device that quickly switches from absorbing to transmitting, suddenly reducing cavity losses.
The Q-switch pulse length is given by
where t is the round trip time (back and forth in the cavity), and R is the output mirror reflectivity ( >98% ).
Therefore
where L is the distance between the mirrors, n1 is the refractive index of the medium, and c is the speed of light. Pulse length can then be written as
Using the data from your laser, what is the theoretical value for the pulse length?
TEM Modes
Set up a camera with the screen at about 1 to 2 meters from the output mirror. Adjust the output coupler screws (or any other adjustments) to produce the TEM00m, TEM10m, TEM01m, .... modes. Photograph or sketch a few of them.
Beam Profile of the TEMoom and the TEM10m modes
Realign the beam to produce the TEMoom mode.
You will use a rotating mirror and a photodiode monitored on an oscilloscope to observe the profile of the laser beam.
Be sure to ensure the photodiode is not saturating when the laser is aligned onto it. If it is, switch the scale of the photodiode amplifier to a lower gain setting.
Repeat your observations for the TEMo1m mode. Remember that photodetectors are square-law detectors, i.e., the current density J is proportional to the square of the electric field. (See Preston for details). Sketch the beam profiles for both modes.
Beam Profile or Shape
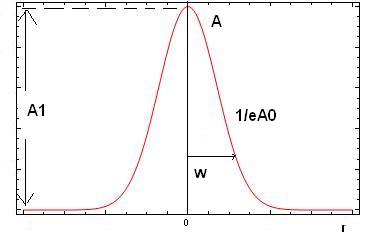
A laser beam has a certain profile with most energy concentrated at the center. The beam has the following form
|
Figure 1 - Amplitude distribution across laser beam oscillating in the TEMoo mode.
|
where w is the radius of the beam. The Gaussian function, exp [- (r/w)2 ] falls to 1/e, when r = w, i.e.,
Since the energy is proportional to the square of the amplitude, the beam radius, or SPOT SIZE, w, is defined as that distance from the axis where the power has dropped to 1/e2 of its value at the center. Twice that distance, 2w, is the beam diameter.
The beam radius, w, is the function of distance along the axis. If we call x the axial distance measured from the midpoint between the two (concave) mirrors, then the parameter w is given by
where λ is the wavelength and w0 is the minimum beam radius between mirrors.
|
|
Note that from wx above; at x = 0, wx = wo.
From Preston (equation 21, p. 102),
Calculate wo and wx.
From your observations of the beam profile for the TEMoom, determine wx, the beam radius. How does your calculated value compare with the experimental value? Explain any differences.
Malus's Law
Malus’ law states that when a linearly polarized light beam of intensity I0 passes through a linear polarizer with its axis rotated by angle A from the light beam polarization, the emergent intensity I is given by
Use the rotatable polarizer and photodiode detector to verify this law quantitatively. Make detector readings at several values of angle A and record them in a neat table in your notebook. Graph your data to demonstrate the expected cos2Adependence.
Verification of the Fresnel-Arago Law
Fresnel-Arago law state that two coherent light rays which are polarized right angles to each other will not mutually interfere.
Use the laser to set up the Michelson interferometer as shown below to form an interference pattern.
Insert polarizers P1 and P2 such that their axes of polarization is in the same direction. You may have to make slight adjustments to retain the interference pattern. Now, rotate ONE of the polarizers through 90º. Verify that the law is true. Try to take pictures of the resulting effect and include them with your report.
References
- ↑ The Art of Experimental Physics, John Wiley and Sons,1991.