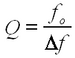Main Page/PHYS 4210/Johnson Noise
Contents
- 1 Johnson Noise
- 2 Introduction
- 3 Procedure
- 3.1 Test of the gain of the pre-amplifier as a function of frequency.
- 3.2 Test of the bandpass filter without using the pre-amplifier.
- 3.3 Test of the amplitude detection unit.
- 3.4 Test of the low-pass filter measurement unit.
- 3.5 Johnson noise measurement.
- 3.6 Large-bandwidth measurement of Johnson noise.
- 3.7 Temeperature dependence of Johnson noise.
- 4 References
Johnson Noise
In this experiment we use an instrumentation amplifier, bandpass filter, and amplitude detector to investigate the noise generated by thermal fluctuations in a resistor, called Johnson noise. Various characteristics of this noise are investigated such as the dependence of the RMS noise voltage on the resistor value, on the bandwidth selected by the filter, and also on temperature.
Key Concepts
|
|
Introduction
Thermal fluctuations are usually investigated in the context of the Brownian motion of molecules (e.g., in the Millikan oil drop experiment), but they permeate other branches of physics. In this experiment we investigate the manifestations of thermal energy fluctuations at room temperature (energy kT, where k is the Boltzmann constant) in a solid, which can be a resistor made of metal wire or a made of a metal film [1] . It will be demonstrated that the energy available due to kT (on average) are responsible for voltage fluctuations across the resistor. Any resistor in an electronic circuit should be treated not only as a passive element which provides a voltage drop for a current passing through it according to Ohm’s law, but, in fact, also as a generator of so-called white noise. Thus, the present experiment not only serves to demonstrate the wonders of physics at non-zero temperature, but also demonstrates the practical importance: noise is unavoidable, one has to make efforts to minimize its effect.
The term white noise refers to the frequency characteristic: in principle, such noise has equal amplitude at all frequencies. In practice, there is a cut-off at high frequencies: when the frequencies f are so high that the quantum energy E = hf becomes comparable to the average thermal energy kT the classical approximation breaks down, and the spectral power density decreases, instead of remaining constant. This resolves the problem of an infinite total power which one would obtain, if the constant power density was integrated over all frequencies to infinity. At the frequencies considered in this laboratory, however, the spectral density is constant (calculate the critical frequency where quantum effects will kick in).
Nyquist [2] provided a consistent explanation for resistor noise. Derivations are offered in Statistical and Thermal Physics textbooks [3]. The root mean square (RMS) noise voltage is given as
| (1) |
Here R is the resistance, and Δf the bandwidth of the noise which has to be defined in some way, as the noise signal is usually measured over a finite frequency range, which usually, however, is not described by a simple square profile (minimum and maximum frequency). One can use for the bandwidth definition the points where the other wise flat transmission curve (ratio of output to input voltage) falls by 3 dB (understand what that means).
Johnson noise is not associated with the flow of current through the device. Other types of noise are:
- shot noise (e.g., in semiconductor devices and vacuum tubes, cf.. separate experiment), which is also white, and depends on the magnitude of the current, and is a manifestation of the quantization of charge;
- flicker noise or 1/f noise, which is an incompletely understood phenomenon common to amplifiers, and which includes low-frequency drifts that plague DC measurements in particular;
- interference noise, such as 60-cycle AC noise and its harmonics, radio frequency noise provided by radio stations, cell phones, etc. , cosmic radiation, transients associated with equipment being turned on or off, to name a few [4].
Life can be complicated for experimentalists!
For the experimental verification of this law one uses the following electronic modules:
- a pre-amplifier with high gain, and low intrinsic noise
- an amplifying (active) bandpass filter of variable bandwidth Δf, which is related to the quality factor according to (f0 is the centre frequency)
(2) - a full-wave precision rectifier, which turns an AC signal into a positive signal (possibly with additional selectable gain)
- a low-pass filter to integrate the rectified signal and thereby measure the RMS voltage.
These modules are contained in the TeachSpin Signal Processor/Lock-in Amplifier [5]. Figure 1 shows the front panel of the apparatus.
One of the functions of this experiment is to prepare you for the more sophisticated lock-in amplifier experiment. In parts 1-4 of the procedure you are asked to measure the characteristics of some of the modules. You will also use an oscilloscope to monitor the signals. It is possible with the high gain settings on the amplifier stages to oversaturate the signal (it will be clipped at about +/- 10 V), and only a careful monitoring of the signal at intermediate stages with an oscilloscope can prevent that from happening.
|
|
Procedure
Test of the gain of the pre-amplifier as a function of frequency.
Use a signal generator and the dual-trace oscilloscope to measure the ratio of pre-amplifier output over input as a function of frequency. Use an external signal generator which can reach frequencies higher than the built-in generator, such that you can observe roll-off at high frequencies (loss of gain). Use the measurement function of the TDS210 digital storage oscilloscope (DSO) to measure the gain (to few-percent accuracy), and compare with some of the gain settings. You will need to use an attenuated output from the signal generator, and use sine waves for the measurement. At a high-frequency setting where the pre-amplifier demonstrates a loss in gain observe what happens to a triangle or square wave (print a screenshot), and explain why the shape of the output signal is distorted. Explore the difference between AC and DC settings on input of the pre-amplifier (you may need to explore very low frequencies to appreciate the high-pass behaviour of the AC setting).
Test of the bandpass filter without using the pre-amplifier.
Measure the ratio of output over input as a function of frequency for a given quality factor Q setting using two traces on the oscilloscope and the MEASURE function. Also measure the phase shift of the output with respect to the input at the same frequencies and for the same Q setting, and discuss the two graphs in your report. It makes sense to overlay the graphs. Be careful when reading centre frequency from the dial/switch combination. Use the frequency measurement option on the DSO to check your reading of the dial.
Test of the amplitude detection unit.
Note that the lock-in/amplitude switch always remains in the setting for amplitude detection in this laboratory. The gain of the detector can be increased. The reference oscillator input is not used in amplitude detection mode. Observe on the oscilloscope the traces of signal input and output, verify that you measure a full-wave rectified input signal. You may want to check the accuracy of the gain settings at a typical frequency in the kHz range.
Test of the low-pass filter measurement unit.
Keep the set-up from the previous section, but in addition to observing input and rectified signals (the latter enhanced by the gain factor) connect the output from the amplitude detector to the low-pass measurement unit. The purpose here is to perform a DC measurement of the RMS voltage. The unit offers the possibility of additional gain, but note that the analog instrument is delicate, and should not be driven beyond its maximum range (to preserve its accuracy for future generations of students!). An output is available for connection of an analog or digital voltmeter (DVM), or to a computer interface. Note that the panel instrument does not offer an absolute scale. The DVM is helpful in order to obtain absolute readings, but not essential if the rectified output is monitored on the oscilloscope (which has RMS measurement functions). You may want to measure the output from the low-pass filter unit (using DVM or DSO), however, as it makes use of the selectable time constant of the low-pass filter, i.e., one has control in case the result is fluctuating. Note that absolute readings of the RMS voltage are only meaningful in the context of also noting the gain settings of the three switches (pre-amplifier – in case used, amplitude detector, low-pass filter), as well as the Q value of the bandpass.
Johnson noise measurement.
Connect the pre-amplifier to the set-up from the previous section, and remove the signal generator. Connect a resistor across the input (e.g., to the positive input terminal against ground, while the negative input is grounded using the switch close to the BNC connector). First, select the positive input also to be grounded by the switch on the panel below the BNC connector. Start with gain settings of unity. Increase the gain to the point where a reading is obtained on the panel instrument. The measurement of the RMS noise voltage for zero resistance across the input represents the contribution from the entire amplifier. Note how you can measure it at different center frequencies f0 for a given Q setting, and how it is largely independent of the chosen value f0. Note how at fixed f0 the RMS voltage changes with the setting of Q. Most of the noise originates in the low-noise pre-amplifier. In Ref. [5], page 30 specifications are provided for the pre-amp, the listing for the noise at f0 = 1 kHz is 9 nV/sqrt(Hz). Note that the RMS noise voltage reading scales with the square root of the bandwidth. Use a voltmeter or the DSO connected to the BNC output from the low-pass filter measurement unit to determine the absolute voltage reading there. Use the gain settings to calculate the corresponding voltage at the input of the pre-amp. Compare your findings with the specification at 1 kHz, and measure the pre-amp noise also at a few other frequencies. Use eq. (2) to translate Q and f0 into a bandwidth value.
Now connect different resistors R across the input. While changing resistors ensure that the switch is set to the grounded position (this will ensure that the panel meter will be saved from the needle banging against its boundaries). You should collect tables of RMS voltage readings as a function of R for different choices of Q. The square of the RMS voltage when graphed against R should be fitted to a straight line (with non-zero y-intercept, i.e., a finite reading at 'R=0 for the amplifier noise voltage). Amplifier input noise current should be negligible for the relatively small resistances. The amplifier has an input impedance of 1 MOhm, which means that one can ignore it, as long as R does not exceed a small fraction of it (e.g., 100 kOhms). The graph shows that the amplifier noise voltage and the Johnson noise voltage are to be added in quadrature. From these results you should be able to establish the dependence of the Johnson RMS noise voltage on resistance, and on bandwidth.
When observing the noise signal at the output from the bandpass filter note how it shows up with a regular, almost sinusoidal shape. This is the result of the narrow bandpass filter (particularly at high Q settings) allowing through only signals with frequencies close to f0. These filtered noise components do have random phases. An analogue to these signals would be in optics the observation of nearly monochromatic light from an incandescent lamp through a narrow filter. One can then do interference measurements with this light. When you reduce the Q value, you can observe how the filtered signal acquires more randomness. A much larger fraction of the noise spectrum is observed in the next section.
Large-bandwidth measurement of Johnson noise.
It is also possible to measure the Johnson noise over a wider range of frequencies. One can use the frequency points at which the gain characteristic falls to the -3dB level as the points which characterize the bandwidth, i.e., as the lower and upper limits of the frequency range. Thus, the pre-amplifier when operated in DC mode still acts as a low-pass filter. The -3dB roll-off point at high frequencies are listed for the pre-amp, e.g., for the gain setting of 1000 it is 10.4 kHz (cf.. [5], p.35). For the amplitude detector we will choose a gain of 100, for which the 3 dB roll-off point is at 44 kHz(cf.. [5], p.30), i.e., irrelevant in the present context. Connect the pre-amplifier output directly to the amplitude detector unit. Use the amplitude detector in AC mode, which provides a high-pass with a frequency cut-off at 3 Hz (3dB roll off). This avoids the signal being affected by DC offset of the pre-amplifier. Together the low-pass pre-amplifier, and the high/low pass amplitude detector form a bandpass filter with a large bandwidth.
Keep the positive input of the pre-amplifier open, and the negative input closed. This corresponds to a resistor of 1 MOhm across the input which is built into the pre-amplifier circuit and which defines the input impedance of the pre-amp. Set the pre-amplifier gain to 1000, and the amplitude detector gain to 100 for and overall gain of 105. According to the comments made about the roll-off points this will correspond to a bandwidth of 10.4 kHz. Observe the signal output from the pre-amplifier, as well as the amplitude detector output on the oscilloscope. In contrast to the previous measurements with the bandpass filter unit you will see random noise signals at various frequencies, as the bandwidth Δf is now fairly wide. The 3dB roll-off point of the pre-amp as given in the manual, should correspond to the results measured in 1. Measure the output RMS using a DC voltmeter (or the DSO) following the low-pass filter unit. The measured voltage when divided by the combined gain factor (105) yields the noise voltage, and should be compared to eq. (1). This complements the measurement taken at selected narrow-bandpass frequencies. It can be repeated with an external resistor across the input. The operational amplifier at the heart of the pre-amp has a higher input impedance than the 1 MOhm resistor that is built in internally across the input. Why do you think does one want to limit the impedance of the instrument by putting a resistor across the input?
Temeperature dependence of Johnson noise.
For a final experiment ask for a styrofoam cup of liquid nitrogen, and an insulated resistor mounted in an epoxy and connected to a BNC cable. First measure the Johnson noise for this resistor at room temperature, and note how it corresponds to a data point on one of your curves (for a given bandwidth setting controlled by f0 and Q). While measuring the RMS noise voltage dip the resistor into liquid nitrogen, and observe what happens to the noise level. For a metal film resistor one has a small dependence of the value of R on temperature. This can be verified independently by using the DVM in resistance measurement mode and measuring the resistance at room temperature as well as at liquid nitrogen temperature (77 ? K). How does your result for the drop in noise voltage compare with the expectation according to eq. (1). Do not forget about the independent amplifier noise in your analysis, if it is relevant at all.
Concerning error analysis: obviously there are very numerous sources of error. Some of these are easily taken care of, others are not. The initial parts of the procedure provide you with a notion that the gain settings are perhaps accurate at the few-percent level (at frequencies up to a few kHz). If the readings for the RMS voltage fluctuate over time, you can help yourself by increasing the time constant, but there still may be longer-term fluctuations. In this case the reading will introduce the biggest uncertainty. The Q factor setting is also a potential source of significant error.
References
- ↑ J.B. Johnson, Thermal Agitation of Electricity in Conductors, Phys. Rev. 32, 97-109 (1928).
- ↑ H. Nyquist, Thermal Agitation of Electric Charge in Conductors, Phys. Rev. 32, 110-113 (1928).
- ↑ Wannier, Statistical Mechanics, Wiley 1966 (also: Dover reprint), chapter 23; also: Kittel-Kroemer.
- ↑ Horowitz and W. Hill, The Art of Electronics, Cambridge University Press 1989, 2nd ed., chapter 7.11
- ↑ 5.0 5.1 5.2 5.3 TeachSpin Signal Processor/Lock-in Amplifier Documentation (it includes a pedagogical review of noise, and a glossary of electronic terms).