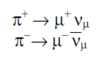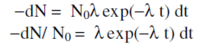Difference between revisions of "Main Page/PHYS 4210/Muon Lifetime"
| Line 68: | Line 68: | ||
is λdt, where λ is a constant “decay rate” that characterizes how rapidly a muon decays, | is λdt, where λ is a constant “decay rate” that characterizes how rapidly a muon decays, | ||
then the change dN in our population of muons is just dN = −N(t)λ dt, or dN/N(t) = −λdt. | then the change dN in our population of muons is just dN = −N(t)λ dt, or dN/N(t) = −λdt. | ||
| − | Integrating, we have N(t) = | + | Integrating, we have N(t) = N<sub>0</sub>exp(−λ t), where N(t) is the number of surviving muons at |
| − | some time t and | + | some time t and N<sub>0</sub> is the number of muons at t = 0. The "lifetime" t of a muon is the |
reciprocal of λ, t = 1/λ. This simple exponential relation is typical of radioactive decay.</p> | reciprocal of λ, t = 1/λ. This simple exponential relation is typical of radioactive decay.</p> | ||
| Line 77: | Line 77: | ||
distribution has a simple exponential form of the type described above. By decay time | distribution has a simple exponential form of the type described above. By decay time | ||
distribution D(t), we mean that the time-dependent probability that a muon decays in the | distribution D(t), we mean that the time-dependent probability that a muon decays in the | ||
| − | time interval between t and t + dt is given by D(t)dt. If we had started with | + | time interval between t and t + dt is given by D(t)dt. If we had started with N<sub>0</sub> muons, |
| − | then the fraction −dN/ | + | then the fraction −dN/N<sub>0</sub> that would on average decay in the time interval between t and |
t + dt is just given by differentiating the above relation: | t + dt is just given by differentiating the above relation: | ||
<table width=200 align=center> | <table width=200 align=center> | ||
| Line 86: | Line 86: | ||
</td><td> <b>(2)</b></td></tr></table> | </td><td> <b>(2)</b></td></tr></table> | ||
The left-hand side of the last equation is nothing more than the decay probability we | The left-hand side of the last equation is nothing more than the decay probability we | ||
| − | seek, so D(t) = l exp(−λ t). This is true regardless of the starting value of | + | seek, so D(t) = l exp(−λ t). This is true regardless of the starting value of N<sub>0</sub>. That is, the |
distribution of decay times, for new muons entering our detector, is also exponential with | distribution of decay times, for new muons entering our detector, is also exponential with | ||
the very same exponent used to describe the surviving population of muons. Again, what | the very same exponent used to describe the surviving population of muons. Again, what | ||
| − | we call the muon lifetime is t = 1/λ. | + | we call the muon lifetime is t = 1/λ.</p> |
| − | </p> | + | <p>Because the muon decay time is exponentially distributed, it does not matter that the |
| + | muons whose decays we detect are not born in the detector but somewhere above us in | ||
| + | the atmosphere. An exponential function always “looks the same” in the sense that | ||
| + | whether you examine it at early times or late times, its e-folding time is the same.</p> | ||
<h1>References</h1> | <h1>References</h1> | ||
<references/> | <references/> | ||
Revision as of 14:40, 15 November 2012
Contents
Muon Lifetime
Introduction
The muon is one of nature’s fundamental “building blocks of matter” and acts in many ways as if it were an unstable heavy electron, for reasons no one fully understands. Discovered in 1937 by C.W. Anderson and S.H. Neddermeyer when they exposed a cloud chamber to cosmic rays, its finite lifetime was first demonstrated in 1941 by F. Rasetti. The instrument described in this manual permits you to measure the charge averaged mean muon lifetime in plastic scintillator, to measure the relative flux of muons as a function of height above sea-level and to demonstrate the time dilation effect of special relativity. The instrument also provides a source of genuinely random numbers that can be used for experimental tests of standard probability distributions.
Our Muon Source
The top of earth's atmosphere is bombarded by a flux of high energy charged particles produced in other parts of the universe by mechanisms that are not yet fully understood. The composition of these "primary cosmic rays" is somewhat energy dependent but a useful approximation is that 98% of these particles are protons or heavier nuclei and 2% are electrons. Of the protons and nuclei, about 87% are protons, 12% helium nuclei and the balance are still heavier nuclei that are the end products of stellar nucleosynthesis. [1]
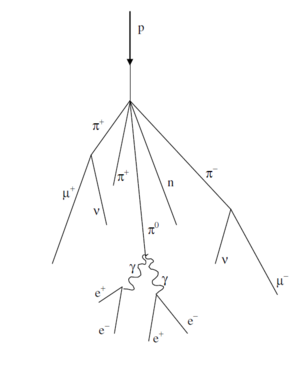
The primary cosmic rays collide with the nuclei of air molecules and produce a shower of particles that include protons, neutrons, pions (both charged and neutral), kaons, photons, electrons and positrons. These secondary particles then undergo electromagnetic and nuclear interactions to produce yet additional particles in a cascade process. Figure 1 indicates the general idea. Of particular interest is the fate of the charged pions produced in the cascade. Some of these will interact via the strong force with air molecule nuclei but others will spontaneously decay (indicated by the arrow) via the weak force into a muon plus a neutrino or antineutrino:
| (1) |
The muon does not interact with matter via the strong force but only through the weak and electromagnetic forces. It travels a relatively long instance while losing its kinetic energy and decays by the weak force into an electron plus a neutrino and antineutrino. We will detect the decays of some of the muons produced in the cascade. (Our detection
efficiency for the neutrinos and antineutrinos is utterly negligible.)
|
Figure 1- Cosmic ray cascade induced by a cosmic ray proton striking an air molecule
nucleus.
|
Not all of the particles produced in the cascade in the upper atmosphere survive down to sea-level due to their interaction with atmospheric nuclei and their own spontaneous decay. The flux of sea-level muons is approximately 1 per minute per cm2 (see [2] for more precise numbers) with a mean kinetic energy of about 4 GeV.
Careful study [3] shows that the mean production height in the atmosphere of the muons detected at sea-level is approximately 15 km. Travelling at the speed of light, the transit time from production point to sea-level is then 50 μsec. Since the lifetime of at-rest muons is more than a factor of 20 smaller, the appearance of an appreciable sealevel muon flux is qualitative evidence for the time dilation effect of special relativity.
Muon Decay Time Distribution
The decay times for muons are easily described mathematically. Suppose at some time t we have N(t) muons. If the probability that a muon decays in some small time interval dt is λdt, where λ is a constant “decay rate” that characterizes how rapidly a muon decays, then the change dN in our population of muons is just dN = −N(t)λ dt, or dN/N(t) = −λdt. Integrating, we have N(t) = N0exp(−λ t), where N(t) is the number of surviving muons at some time t and N0 is the number of muons at t = 0. The "lifetime" t of a muon is the reciprocal of λ, t = 1/λ. This simple exponential relation is typical of radioactive decay.
Now, we do not have a single clump of muons whose surviving number we can easily measure. Instead, we detect muon decays from muons that enter our detector at essentially random times, typically one at a time. It is still the case that their decay time distribution has a simple exponential form of the type described above. By decay time distribution D(t), we mean that the time-dependent probability that a muon decays in the time interval between t and t + dt is given by D(t)dt. If we had started with N0 muons, then the fraction −dN/N0 that would on average decay in the time interval between t and t + dt is just given by differentiating the above relation:
| (2) |
The left-hand side of the last equation is nothing more than the decay probability we seek, so D(t) = l exp(−λ t). This is true regardless of the starting value of N0. That is, the distribution of decay times, for new muons entering our detector, is also exponential with the very same exponent used to describe the surviving population of muons. Again, what
we call the muon lifetime is t = 1/λ.
Because the muon decay time is exponentially distributed, it does not matter that the muons whose decays we detect are not born in the detector but somewhere above us in the atmosphere. An exponential function always “looks the same” in the sense that whether you examine it at early times or late times, its e-folding time is the same.
References
- ↑ Simpson, J.A., "Elemental and Isotopic Composition of the Galactic Cosmic Rays", in Rev. Nucl. Part. Sci., 33, pp. 323.
- ↑ Particle Data Group
- ↑ Particle Data Group