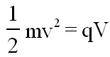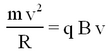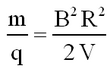Difference between revisions of "Main Page/PHYS 4210/Mass Spectrometer"
| Line 63: | Line 63: | ||
</ul> | </ul> | ||
<p>Note that the magnetic field strength B is measured in Tesla (in MKSA units). (The Earth's magnetic field has a strength on the order of 1 Gauss = 10<sup>-4</sup> T). By reading the voltage at the peaks for a particular magnetic field, and substituting into equation (3), it is possible to identify the isotope(s) [use Maple or Mathematica].</p> | <p>Note that the magnetic field strength B is measured in Tesla (in MKSA units). (The Earth's magnetic field has a strength on the order of 1 Gauss = 10<sup>-4</sup> T). By reading the voltage at the peaks for a particular magnetic field, and substituting into equation (3), it is possible to identify the isotope(s) [use Maple or Mathematica].</p> | ||
| + | |||
| + | <p>A typical I-V plot for fixed B looks as follows (identity of peaks removed):</p> | ||
| + | <table width=500 align=center><td> | ||
| + | <p align=justify>[[File:Mspec-fig2.png|500px|border|center]] | ||
| + | <b>Figure 2 -</b> A typical mass spectrum. | ||
| + | <br clear=right> | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <p>We provide a table with atomic weights for a few atoms that might appear in your spectrum. Consult a table of isotopes that can be found at the back of any Modern Physics text or in the CRC handbook.</p> | ||
| + | <table align=center> | ||
| + | <tr><td><b>Isotope</b></td> <td><b>Atomic Weight</b></td></tr> | ||
| + | <tr><td><sup>1</sup>H </td> <td>1.008</td></tr> | ||
| + | <tr><td><sup>4</sup>He </td> <td>4.004</td></tr> | ||
| + | <tr><td><sup>6</sup>Li </td> <td>6.017</td></tr> | ||
| + | <tr><td><sup>7</sup>Li </td> <td>7.018</td></tr> | ||
| + | <tr><td><sup>7</sup>LiH </td> <td>8.026</td></tr> | ||
| + | <tr><td><sup>9</sup>Be </td> <td>9.015</td></tr> | ||
| + | <tr><td><sup>12</sup>C </td> <td>12.004</td></tr> | ||
| + | <tr><td><sup>14</sup>N </td> <td>14.008</td></tr> | ||
| + | <tr><td><sup>16</sup>O </td> <td>16.000</td></tr> | ||
| + | <tr><td><sup>23</sup>Na </td> <td>22.990</td></tr> | ||
| + | <tr><td><sup>24</sup>Mg </td> <td>24.312</td></tr> | ||
| + | <tr><td><sup>28</sup>Si </td> <td>28.977</td></tr> | ||
| + | <tr><td><sup>32</sup>S </td> <td>31.972</td></tr> | ||
| + | <tr><td><sup>39</sup>K </td> <td>38.964</td></tr> | ||
| + | <tr><td><sup>40</sup>Ca </td> <td>39.363</td></tr> | ||
| + | <tr><td><sup>41</sup>K </td> <td>40.962</td></tr> | ||
| + | </table> | ||
Revision as of 12:27, 8 August 2011
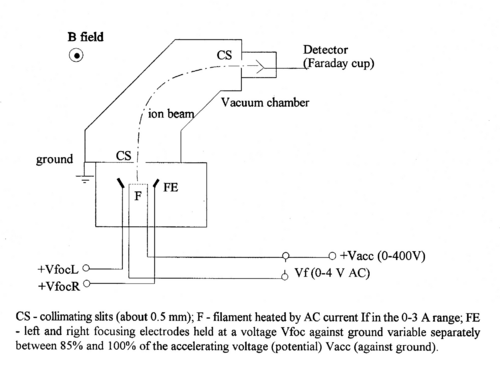
Mass Spectrometer
The mass spectrometer is a device that separates and identifies ions according to their mass-to-charge ratio using the linear acceleration and deflection of ions, in electric and magnetic fields respectively.
|
Figure 1 - Schematic diagram of the magnetic selector mass spectrometer.
|
Key Concepts
- Charge-to-mass ratio
- A/D Converter
- Mean free path
- Faraday Cup
- Diffusion pump
- magnetic selector
- Roughing pump
- Ion gauge
- Thermocouple gauge
Pre-Lab Requirement
This experiment has a prelab component. You must complete this exercise before you meet the TA for a demonstration.
Prepare a table of showing at which accelerating voltage you would expect to see a signal for the isotopes listed in the table below. Provide these for various values of magnetic field between 0.1T and 0.3T.
For example:
| 0.1 T | 0.12 T | 0.14 T | ... | |
| 1H | ||||
| 4He | ||||
| 6Li | ||||
| 7Li | ||||
| ... |
Theory
A filament coated with a salt (e.g. sodium sulfate) when heated, produces neutral atoms and ions (e.g., Na+). This process of surface ionization works if the ionization potential of the atom is not too large compared to the work function of the metal (cf.. ref. 1).
In turn these ions are accelerated towards collimating slit by a potential difference V, and acquire a (small) kinetic energy of
| (1) |
where q, m, and v are the charge, mass and velocity of the ions respectively.
Some ions pass through the collimating slit and into the homogeneous magnetic field of strength B, this field will deflect them into circular paths of radius R such that the centrifugal and magnetic forces balance. For this condition we have:
| (2) |
Thence from eqs. 1 and 2 the mass-to-charge ratio is given by
| (3) |
The value of R is fixed by the geometry of the spectrometer. In practice there is a problem with determining its accurate value, since the magnetic field has fringes both where the ions enter and exit. Therefore, it is not simply determined by the size of the magnet, but an effective radius has to be determined. By varying B or V, ions with different mass-charge ratios can be collected.
Assuming singly charged ions (q = 1e) and a radius that is fixed by the size of the magnet, we see that knowledge of V and B allows us to identify the mass of a given isotope.
- e = 1.60 x 10-19 Coulombs
- R = 4.8 x 10-2 meters (you may have to calibrate for a known mass number)
- m = atomic weight in a.m.u., and 1 a.m.u. = 1.66 x 10-27 kg.
Note that the magnetic field strength B is measured in Tesla (in MKSA units). (The Earth's magnetic field has a strength on the order of 1 Gauss = 10-4 T). By reading the voltage at the peaks for a particular magnetic field, and substituting into equation (3), it is possible to identify the isotope(s) [use Maple or Mathematica].
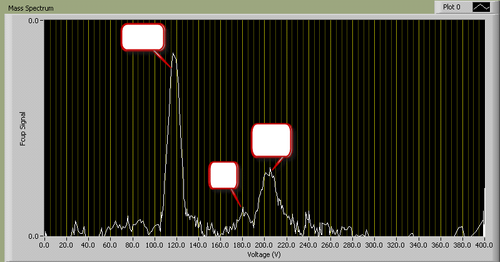
A typical I-V plot for fixed B looks as follows (identity of peaks removed):
|
Figure 2 - A typical mass spectrum.
|
We provide a table with atomic weights for a few atoms that might appear in your spectrum. Consult a table of isotopes that can be found at the back of any Modern Physics text or in the CRC handbook.
| Isotope | Atomic Weight |
| 1H | 1.008 |
| 4He | 4.004 |
| 6Li | 6.017 |
| 7Li | 7.018 |
| 7LiH | 8.026 |
| 9Be | 9.015 |
| 12C | 12.004 |
| 14N | 14.008 |
| 16O | 16.000 |
| 23Na | 22.990 |
| 24Mg | 24.312 |
| 28Si | 28.977 |
| 32S | 31.972 |
| 39K | 38.964 |
| 40Ca | 39.363 |
| 41K | 40.962 |