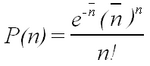Difference between revisions of "Main Page/PHYS 3220/Radioactive Decays"
| (44 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
<h1>Radioactive Decays</h1> | <h1>Radioactive Decays</h1> | ||
| − | < | + | <h1>Learning Outcomes</h1> |
| + | <ol> | ||
| + | <li>Three types of radioactivity | ||
| + | <li>Poisson statistics | ||
| + | <li>Radiation detection technology | ||
| + | </ol> | ||
<h1>Introduction</h1> | <h1>Introduction</h1> | ||
| Line 10: | Line 15: | ||
<ol style="list-style-type:lower-roman"> | <ol style="list-style-type:lower-roman"> | ||
<li><p><b>α-decay:</b> heavy radionucleides often decay via the emission of a cluster composed of 2 protons and 2 neutrons, i.e., a <sub>2</sub>He<sup>4</sup> nucleus.</p></li> | <li><p><b>α-decay:</b> heavy radionucleides often decay via the emission of a cluster composed of 2 protons and 2 neutrons, i.e., a <sub>2</sub>He<sup>4</sup> nucleus.</p></li> | ||
| − | <li><p><b>β-decay:</b> nuclei away from the line of stability N = Z, where N is the total number of neutrons, and Z the total number of protons, can lower their energy, and hence become more stable by emitting either an electron or a positron. In the case of neutron-rich nuclei a fast electron is emitted from the nucleus, | + | <li><p><b>β-decay:</b> nuclei away from the line of stability N = Z, where N is the total number of neutrons, and Z the total number of protons, can lower their energy, and hence become more stable, by emitting either an electron or a positron. In the case of neutron-rich nuclei, a neutron converts into a proton, electron and antineutrino. The fast electron is emitted from the nucleus, corresponding to the β<sup>-</sup> decay of free neutrons (half-life 10.6 min.). For proton-rich nuclei, a proton is converted into a neutron, positron and a neutrino (β<sup>+</sup> decay). The fast positron emerges from the nucleus. This latter process may seem counterintuitive as it cannot occur for free protons (why?). The rest of the nuclear system supplies the energy necessary for the reaction to take place.</p></li> |
| − | <li><p><b>γ-decay:</b> the emission of photons with higher | + | <li><p><b>γ-decay:</b> the emission of photons with energies higher than X-rays (MeV-range) is the result of a nuclear transition from an excited to a lower state in complete analogy with photon emission from excited atoms (eV to keV-range). This decay almost always accompanies α- and β-decays, since these processes usually leave the daughter nucleus in an excited state.</p></li> |
<li><p><b>spontaneous fission:</b>the emission of nuclear clusters bigger than α-particles is a rare process that has been studied recently in a systematic way at heavy ion facilities. It represents an alternative but rare decay mechanism, which provides insight into the nature of nuclear forces.</p></li> | <li><p><b>spontaneous fission:</b>the emission of nuclear clusters bigger than α-particles is a rare process that has been studied recently in a systematic way at heavy ion facilities. It represents an alternative but rare decay mechanism, which provides insight into the nature of nuclear forces.</p></li> | ||
</ol> | </ol> | ||
| − | <p>All modern physics texts contain a chapter that describes nuclear phenomenology as well as a table of isotopes. Understand the basic principles (there will be no need to | + | <p>All modern physics texts contain a chapter that describes nuclear phenomenology as well as a table of isotopes. Understand the basic principles (there will be no need to understand previous chapters of the book for this!). See, e.g., refs. 1-3. </p> |
<h2>Detection of radiation</h2> | <h2>Detection of radiation</h2> | ||
| − | <p>The detection of nuclear radiation relies on the property that it ionizes the surrounding matter through which it passes. This statement is obvious for the charged α, and β particles. For γ particles the ionization arises through the photoeffect and Compton scattering ( | + | <p>The detection of nuclear radiation relies on the property that it ionizes the surrounding matter through which it passes. This statement is obvious for the charged α, and β particles. For γ particles the ionization arises through the photoeffect and Compton scattering (refs. 1-3). This ionization can be detected through the electric spark induced between condenser plates that are biased with a high voltage, resulting in a short burst of current. This is the principle of a Geiger-Müller (GM) tube. The efficiency of detection depends on the voltage applied to the gas-filled tube (why can’t one use a vacuum tube?). It is important to realize that the detector has a finite efficiency, i.e., it does not detect every single α, β, or γ particle entering the detector. In particular, the efficiency depends on the voltage applied with a threshold behaviour (around 900 V) followed by saturation. In small hand-held radiation counters the high voltage is produced by a DC-DC converter as used in electronic flashlights. Read the description of GM counters available in many texts (e.g., refs. 1,2,6), and include a concise description in your own words in your report.</p> |
<p>Other detection mechanisms used for monitoring are: (i) exposure blackening of photographic film, e.g., in personal total dose monitors; (ii) scintillator counters; (iii) triggering of semiconductor devices; etc. </p> | <p>Other detection mechanisms used for monitoring are: (i) exposure blackening of photographic film, e.g., in personal total dose monitors; (ii) scintillator counters; (iii) triggering of semiconductor devices; etc. </p> | ||
<h2>Absorption of radiation</h2> | <h2>Absorption of radiation</h2> | ||
| − | <p>Radiation is slowed down and eventually stopped | + | <p>Radiation is slowed down and eventually stopped as it passes through matter. This fact is exploited both in shielding and in applications of radiation for energy deposition (e.g., burning of cancer cells in radiation medicine). The absorption of the three different forms of radiation by matter is very different: α particles are heavy and doubly charged, therefore, they give up their energy readily in collisions with the nuclei of the surrounding matter; β particles are lighter and faster (as they emerge from the decay), and therefore pass more readily through matter until they are stopped; γ-rays have the best penetration characteristics, i.e., are the most difficult to shield. α particles, which have typical energies of 5 MeV, are stopped by a few centimeters of air, since they are doubly charged and slow compared to β particles. They are detected by GM counters only if they enter through a specially designed opening (transparent to them provided they are fast enough). </p> |
| − | <p>The stopping power and energy deposition is also a function that depends strongly on the kinetic energy of the ionizing particles. In radiation medicine this is | + | <p>The stopping power and energy deposition is also a function that depends strongly on the kinetic energy of the ionizing particles. In radiation medicine this is exploited, e.g., by having fast particles penetrate healthy tissue with limited damage but sufficient slow-down such that energy deposition becomes efficient when the tissue to be destroyed is reached. Usually physicists with nuclear medicine training are in charge of designing a radiation plan for each patient depending on the location of the tissue to be destroyed, vicinity of vital organs, etc. This is a non-trivial process, since secondary radiation (e.g., production of electrons) contributes to the energy deposition and may diffuse the flux of radiation.</p> |
<h2>Lifetimes of radioactive sources</h2> | <h2>Lifetimes of radioactive sources</h2> | ||
| Line 35: | Line 40: | ||
<h2>Statistics of nuclear counting</h2> | <h2>Statistics of nuclear counting</h2> | ||
| − | <p>In the early studies of radioactivity | + | <p>In the early studies of radioactivity it was not understood whether radioactivity was a purely random process, or whether the emission of one particle might effect the emission of others. One can prove that the observation of the number of independent decays per time interval (count rate) as a function of time should result in a Poissonian distribution (ref. 5). In the limit of high count rates the Poissonian distribution can be approximated by a Gaussian distribution. </p> |
| − | <p>Rutherford performed experiments | + | |
| + | <p>Rutherford performed experiments that showed that the probability, ''P(n)'', of observing ''n'' counts in a fixed time interval followed the Poisson formula</p> | ||
<table width=400 align=center> | <table width=400 align=center> | ||
| Line 51: | Line 57: | ||
</td></table> | </td></table> | ||
| − | <p>For all the measurements in this experiment that are performed with computerized data acquisition and data analysis, the Poissonian character of the statistical distribution of decay events are to be investigated and verified. Since the computer program | + | <p>For all the measurements in this experiment that are performed with computerized data acquisition and data analysis, the Poissonian character of the statistical distribution of decay events are to be investigated and verified. Since the computer program "Particle Tracking.vi" performs the statistical analysis automatically, it is crucial that you think through the steps involved in obtaining the histogram (ch. 11 in ref. 5).</p> |
<p>To illustrate how one explicitly analyzes the data we include an example for your convenience.</p> | <p>To illustrate how one explicitly analyzes the data we include an example for your convenience.</p> | ||
| Line 57: | Line 63: | ||
<ol> | <ol> | ||
<li>Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below). | <li>Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below). | ||
| − | <table width= | + | <table width=420 align=center> |
| − | <tr><td><b>Number of Counts in interval (n)</b></td><td><b> | + | <tr><td width=120><b>Number of Counts in interval (n)</b></td><td width=120><b>Number of times Count occurs</b></td><td width=100><b>''P(n)''</b></td><td width=100><b>Total Counts</b></td></tr> |
<tr><td>0</td> <td>I(1)</td> <td>0.01</td> <td>0x1=0</td></tr> | <tr><td>0</td> <td>I(1)</td> <td>0.01</td> <td>0x1=0</td></tr> | ||
| − | <tr><td>1</td> <td> | + | <tr><td>1</td> <td>III(3)</td> <td>0.03</td> <td>1x3=3</td></tr> |
<tr><td>2</td> <td>IIII I(5)</td> <td>0.05</td> <td>2x5=10</td></tr> | <tr><td>2</td> <td>IIII I(5)</td> <td>0.05</td> <td>2x5=10</td></tr> | ||
<tr><td>etc..</td><td></td><td></td><td></td></tr> | <tr><td>etc..</td><td></td><td></td><td></td></tr> | ||
</table> | </table> | ||
</li> | </li> | ||
| + | |||
| + | <li><p>Now construct a bar graph for the results, showing ''P(n)'' vs ''n'', where ''P(n)'' is the probability for finding n counts:</p> | ||
| + | <table width=400 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Rd-eqn3.png|260px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <p>Then, using the Poisson distribution (Eq. 1) evaluate ''P(n)'' and graph the theoretical distribution over the same range of values. To do this, you require the value of n-bar; this should be the mean number of counts in your measurement:</p> | ||
| + | <table width=400 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Rd-eqn4.png|110px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <p>Thus, your theoretical distribution and your experimental results will have the same mean.</p> | ||
| + | </li> | ||
| + | <li><p>Now calculate the standard deviation of your data:</p> | ||
| + | <table width=400 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Rd-eqn5.png|180px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | </li> | ||
| + | |||
| + | <li><p>Compare this with the expected standard deviation from the theoretical probability distribution, which is (for a Poisson distribution):</p> | ||
| + | <table width=400 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Rd-eqn6.png|140px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <p>Note that this simple relation between the '''mean''' and the standard deviation is not a property of all distributions.</p> | ||
| + | </li> | ||
| + | |||
| + | <li><p>To see if the numbers of counts obey Poisson statistics in a quantitative way, we use the Chi-squared (χ<sup>2</sup>) test (ch. 12 in ref. 5; an example is given on pg. 235). From the reduced χ<sup>2</sup> value one infers the agreement.</p> | ||
| + | </li> | ||
| + | |||
| + | </ol> | ||
| + | |||
| + | <h1>Experimental Procedure</h1> | ||
| + | |||
| + | <p>In this experiment a Geiger-Müller counter with a computer interface is used to detect the radiation coming from the natural background, as well as from some weak sources. The statistics of the decays is investigated to confirm the independence of the decay mechanism. The dependence of the count rate on the distance from the source is also investigated. Also, the Geiger-Müller method for detection of radioactivity will be investigated.</p> | ||
| + | |||
| + | <p>Familiarize yourself with the computer-interfaced GM counter and associated computer software.</p> | ||
| + | |||
| + | <h2>Required Components</h2> | ||
| + | <ol> | ||
| + | <li>[[Media:Radioactive-ACratemeter.JPG|AC Powered Table-Top GM Counter]]</li> | ||
| + | <li>[[Media:RDHandHeldGM.JPG|Hand-held GM Counter]]</li> | ||
| + | <li>[[Media:RDBeigeFiesta.JPG|Beige 'Fiesta' Ceramic Dish]]</li> | ||
| + | <li>[[Media:RDOrangeFiesta.JPG|Orange 'Fiesta' Ceramic Dish]]</li> | ||
| + | <li>[[Media:RDMantles.JPG|α,γ Source: <sub>90</sub>Th<sup>232</sup>, Lantern Mantles]]</li> | ||
| + | </ol> | ||
| + | |||
| + | <h2>Hardware instructions:</h2> | ||
| + | <p>The hand-held GM counter can be operated independent of the computer interface. You should use it in range I (up to 2000? counts per minute - cpm), and turn on the audio monitoring. The background rate should be in the range of up to a few counts per second. For sources we use a bag containing Coleman-type naphta lantern mantles and Fiesta plates. Original Coleman mantles used radioactive elements until 1990; the clones still use a <sub>90</sub>Th<sup>232</sup> α emitter to enhance fluorescence. Radioactive elements were also used in glazing for bathroom tiles and Fiesta plates (no longer on the market). Make sure that the sources are some distance away from the GM counter when measuring the background radiation.</p> | ||
| + | |||
| + | <h2>Computer Instruction</h2> | ||
| + | |||
| + | <p>Data will be collected using a program called "Particle Tracking.vi" located on the desktop. | ||
| + | This program uses the microphone input of the computer to monitor the counts from the "Radiation Alert- Monitor 4" detector. The operation of the program is is described below</p> | ||
| + | |||
| + | <table width=400 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Rd-vi.png|800px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | |||
| + | <p>''Note that the program displays a histogram of the results for you to see, but only the raw data of the counts is written to the output file.''</p> | ||
| + | |||
| + | |||
| + | <h2>Required Data</h2> | ||
| + | <ol> | ||
| + | <li>Test the statistics of nuclear background radiation. Note the direction in which the GM counter is pointing. Make sure that it is aiming at free space, and not at a potential radioactive source. Take at least two runs, one of which should be with a larger amount of data to observe an improvement in the fit to a Poissonian distribution. Comment on the χ<sup>2</sup> obtained, and quote the decay rate, with its standard error. Include histograms of the distributions. Repeat the longer run with the GM counter pointing in an orthogonal direction. Are the data consistent with the previous run? Should they be? What are some sources of background radiation? Save the data points for one of the long runs to a data file. Perform the Poisson statistics analysis explicitly as described in the example in the previous section.</li> | ||
| + | |||
| + | <li>Perform measurements similar to (1) while bringing the bag with lantern mantles (<sub>90</sub>Th<sup>232</sup> α,γ source) close to the opening of the GM counter. Comment on the obtained distribution. Use a detailed table of isotopes (with decay schemes) to identify the radionuclide of the thorium family (ref. 6). </li> | ||
| + | |||
| + | <li>Place the orange 'Fiesta' ceramic dish plate on the table. Mount the GM counter centered above the plate using a retort stand. Measure average count rates as a function of distance, e.g., 0.5 cm, 5 cm, 10 cm, 15 cm, 20 cm, 25 cm. Has the count rate at 25 cm reached the background count rate within errors? Plot the count rates after subtraction of the background rate as a function of distance. What functional behaviour do you find? Can you explain why the Geiger counter is responding when exposed to the Fiesta plate? Show relevant decay chain diagrams.</li> | ||
| + | |||
| + | <li>Turn on the AC powered table-top GM counter. Set the knob to HV and dial up an operating voltage not exceeding 1200 Volts. Set the knob to display count rate X1 (in counts per minute) and note the background radiation. Place the beige Fiesta dish close to the exposed GM tube (the aluminium shield can be rotated such that an opening appears). You may need to reduce the sensitivity of the meter by setting the knob to the X10 range. Then measure the count rate as a function of the operating voltage.</li> | ||
| + | </ol> | ||
| + | |||
| + | <p>Incorporate in your report an outline on the three nuclear decay mechanisms. The function of the GM counter should also be explained briefly in the report.</p> | ||
| + | |||
| + | <h1>References</h1> | ||
| + | |||
| + | <ol> | ||
| + | <li>Knoll, G.F., ''Radiation Detection and Measurement'', 2nd ed.</li> | ||
| + | <li>Tsoulfanidis, N., ''Measurement and Detection of Radiation''.</li> | ||
| + | <li>Rohlf, J.W., ''Modern Physics from α to Z<sup>0</sup>'', Wiley 1994 https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/q36jf8/alma991011387139705164</li> | ||
| + | <li>Thornton, Stephen T., and Andrew F. Rex. Modern Physics for Scientists and Engineers . 3rd ed. Belmont, CA: Thomson, Brooks/Cole, 2006. Print. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/q36jf8/alma991026442989705164 </li> | ||
| + | <li>Brehm J.J., Mullin, W.J. ''Modern Physics'', Wiley 1989</li> | ||
| + | <li>Taylor, J.R., ''An Introduction to Error Analysis'', University Science Books, 1997.</li> | ||
| + | <li>Cork, J.M., ''Radioactivity and Nuclear Physics'', D. van Nostrand 195</li> | ||
</ol> | </ol> | ||
Latest revision as of 12:54, 13 August 2021
Contents
Radioactive Decays
Learning Outcomes
- Three types of radioactivity
- Poisson statistics
- Radiation detection technology
Introduction
Radioactive Decays
Radioactive nuclear decays can be classified according to their decay mechanism:
α-decay: heavy radionucleides often decay via the emission of a cluster composed of 2 protons and 2 neutrons, i.e., a 2He4 nucleus.
β-decay: nuclei away from the line of stability N = Z, where N is the total number of neutrons, and Z the total number of protons, can lower their energy, and hence become more stable, by emitting either an electron or a positron. In the case of neutron-rich nuclei, a neutron converts into a proton, electron and antineutrino. The fast electron is emitted from the nucleus, corresponding to the β- decay of free neutrons (half-life 10.6 min.). For proton-rich nuclei, a proton is converted into a neutron, positron and a neutrino (β+ decay). The fast positron emerges from the nucleus. This latter process may seem counterintuitive as it cannot occur for free protons (why?). The rest of the nuclear system supplies the energy necessary for the reaction to take place.
γ-decay: the emission of photons with energies higher than X-rays (MeV-range) is the result of a nuclear transition from an excited to a lower state in complete analogy with photon emission from excited atoms (eV to keV-range). This decay almost always accompanies α- and β-decays, since these processes usually leave the daughter nucleus in an excited state.
spontaneous fission:the emission of nuclear clusters bigger than α-particles is a rare process that has been studied recently in a systematic way at heavy ion facilities. It represents an alternative but rare decay mechanism, which provides insight into the nature of nuclear forces.
All modern physics texts contain a chapter that describes nuclear phenomenology as well as a table of isotopes. Understand the basic principles (there will be no need to understand previous chapters of the book for this!). See, e.g., refs. 1-3.
Detection of radiation
The detection of nuclear radiation relies on the property that it ionizes the surrounding matter through which it passes. This statement is obvious for the charged α, and β particles. For γ particles the ionization arises through the photoeffect and Compton scattering (refs. 1-3). This ionization can be detected through the electric spark induced between condenser plates that are biased with a high voltage, resulting in a short burst of current. This is the principle of a Geiger-Müller (GM) tube. The efficiency of detection depends on the voltage applied to the gas-filled tube (why can’t one use a vacuum tube?). It is important to realize that the detector has a finite efficiency, i.e., it does not detect every single α, β, or γ particle entering the detector. In particular, the efficiency depends on the voltage applied with a threshold behaviour (around 900 V) followed by saturation. In small hand-held radiation counters the high voltage is produced by a DC-DC converter as used in electronic flashlights. Read the description of GM counters available in many texts (e.g., refs. 1,2,6), and include a concise description in your own words in your report.
Other detection mechanisms used for monitoring are: (i) exposure blackening of photographic film, e.g., in personal total dose monitors; (ii) scintillator counters; (iii) triggering of semiconductor devices; etc.
Absorption of radiation
Radiation is slowed down and eventually stopped as it passes through matter. This fact is exploited both in shielding and in applications of radiation for energy deposition (e.g., burning of cancer cells in radiation medicine). The absorption of the three different forms of radiation by matter is very different: α particles are heavy and doubly charged, therefore, they give up their energy readily in collisions with the nuclei of the surrounding matter; β particles are lighter and faster (as they emerge from the decay), and therefore pass more readily through matter until they are stopped; γ-rays have the best penetration characteristics, i.e., are the most difficult to shield. α particles, which have typical energies of 5 MeV, are stopped by a few centimeters of air, since they are doubly charged and slow compared to β particles. They are detected by GM counters only if they enter through a specially designed opening (transparent to them provided they are fast enough).
The stopping power and energy deposition is also a function that depends strongly on the kinetic energy of the ionizing particles. In radiation medicine this is exploited, e.g., by having fast particles penetrate healthy tissue with limited damage but sufficient slow-down such that energy deposition becomes efficient when the tissue to be destroyed is reached. Usually physicists with nuclear medicine training are in charge of designing a radiation plan for each patient depending on the location of the tissue to be destroyed, vicinity of vital organs, etc. This is a non-trivial process, since secondary radiation (e.g., production of electrons) contributes to the energy deposition and may diffuse the flux of radiation.
Lifetimes of radioactive sources
A proper understanding of nuclear decays on the basis of a nuclear shell model (in analogy to atomic structure of electronic energy levels) enables one to predict the energies of the emitted particles as well as the half-lifes. The lifetime is related to the broadening in energy of the decaying state and can be understood from Heisenberg's uncertainty principle. (As a function of time the number of decaying particles is described by an exponential decay law.)
The radioactive sources that we use in this experiment do not permit a measurement of the decay law, since they have long lifetimes (tens to thousands of years), i.e., it is impossible to observe the decrease in radioactivity over a reasonable time span. However, sources with a short lifetime can be produced by exposure of a sample to a high-flux source, e.g., a reactor, which results in the conversion of stable nuclei into unstable ones.
Statistics of nuclear counting
In the early studies of radioactivity it was not understood whether radioactivity was a purely random process, or whether the emission of one particle might effect the emission of others. One can prove that the observation of the number of independent decays per time interval (count rate) as a function of time should result in a Poissonian distribution (ref. 5). In the limit of high count rates the Poissonian distribution can be approximated by a Gaussian distribution.
Rutherford performed experiments that showed that the probability, P(n), of observing n counts in a fixed time interval followed the Poisson formula
| (1) |
where the average number of counts per interval is calculated as
For all the measurements in this experiment that are performed with computerized data acquisition and data analysis, the Poissonian character of the statistical distribution of decay events are to be investigated and verified. Since the computer program "Particle Tracking.vi" performs the statistical analysis automatically, it is crucial that you think through the steps involved in obtaining the histogram (ch. 11 in ref. 5).
To illustrate how one explicitly analyzes the data we include an example for your convenience.
- Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below).
Number of Counts in interval (n) Number of times Count occurs P(n) Total Counts 0 I(1) 0.01 0x1=0 1 III(3) 0.03 1x3=3 2 IIII I(5) 0.05 2x5=10 etc.. Now construct a bar graph for the results, showing P(n) vs n, where P(n) is the probability for finding n counts:
Then, using the Poisson distribution (Eq. 1) evaluate P(n) and graph the theoretical distribution over the same range of values. To do this, you require the value of n-bar; this should be the mean number of counts in your measurement:
Thus, your theoretical distribution and your experimental results will have the same mean.
Now calculate the standard deviation of your data:
Compare this with the expected standard deviation from the theoretical probability distribution, which is (for a Poisson distribution):
Note that this simple relation between the mean and the standard deviation is not a property of all distributions.
To see if the numbers of counts obey Poisson statistics in a quantitative way, we use the Chi-squared (χ2) test (ch. 12 in ref. 5; an example is given on pg. 235). From the reduced χ2 value one infers the agreement.
Experimental Procedure
In this experiment a Geiger-Müller counter with a computer interface is used to detect the radiation coming from the natural background, as well as from some weak sources. The statistics of the decays is investigated to confirm the independence of the decay mechanism. The dependence of the count rate on the distance from the source is also investigated. Also, the Geiger-Müller method for detection of radioactivity will be investigated.
Familiarize yourself with the computer-interfaced GM counter and associated computer software.
Required Components
- AC Powered Table-Top GM Counter
- Hand-held GM Counter
- Beige 'Fiesta' Ceramic Dish
- Orange 'Fiesta' Ceramic Dish
- α,γ Source: 90Th232, Lantern Mantles
Hardware instructions:
The hand-held GM counter can be operated independent of the computer interface. You should use it in range I (up to 2000? counts per minute - cpm), and turn on the audio monitoring. The background rate should be in the range of up to a few counts per second. For sources we use a bag containing Coleman-type naphta lantern mantles and Fiesta plates. Original Coleman mantles used radioactive elements until 1990; the clones still use a 90Th232 α emitter to enhance fluorescence. Radioactive elements were also used in glazing for bathroom tiles and Fiesta plates (no longer on the market). Make sure that the sources are some distance away from the GM counter when measuring the background radiation.
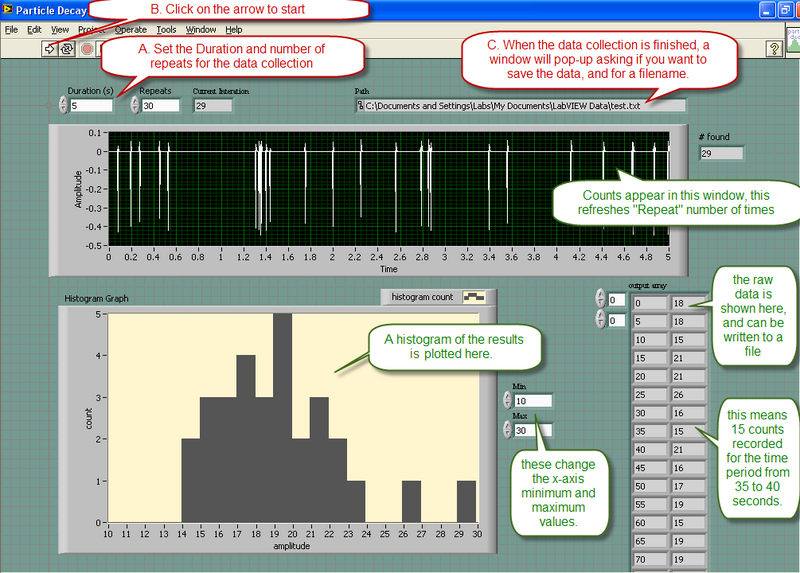
Computer Instruction
Data will be collected using a program called "Particle Tracking.vi" located on the desktop. This program uses the microphone input of the computer to monitor the counts from the "Radiation Alert- Monitor 4" detector. The operation of the program is is described below
Note that the program displays a histogram of the results for you to see, but only the raw data of the counts is written to the output file.
Required Data
- Test the statistics of nuclear background radiation. Note the direction in which the GM counter is pointing. Make sure that it is aiming at free space, and not at a potential radioactive source. Take at least two runs, one of which should be with a larger amount of data to observe an improvement in the fit to a Poissonian distribution. Comment on the χ2 obtained, and quote the decay rate, with its standard error. Include histograms of the distributions. Repeat the longer run with the GM counter pointing in an orthogonal direction. Are the data consistent with the previous run? Should they be? What are some sources of background radiation? Save the data points for one of the long runs to a data file. Perform the Poisson statistics analysis explicitly as described in the example in the previous section.
- Perform measurements similar to (1) while bringing the bag with lantern mantles (90Th232 α,γ source) close to the opening of the GM counter. Comment on the obtained distribution. Use a detailed table of isotopes (with decay schemes) to identify the radionuclide of the thorium family (ref. 6).
- Place the orange 'Fiesta' ceramic dish plate on the table. Mount the GM counter centered above the plate using a retort stand. Measure average count rates as a function of distance, e.g., 0.5 cm, 5 cm, 10 cm, 15 cm, 20 cm, 25 cm. Has the count rate at 25 cm reached the background count rate within errors? Plot the count rates after subtraction of the background rate as a function of distance. What functional behaviour do you find? Can you explain why the Geiger counter is responding when exposed to the Fiesta plate? Show relevant decay chain diagrams.
- Turn on the AC powered table-top GM counter. Set the knob to HV and dial up an operating voltage not exceeding 1200 Volts. Set the knob to display count rate X1 (in counts per minute) and note the background radiation. Place the beige Fiesta dish close to the exposed GM tube (the aluminium shield can be rotated such that an opening appears). You may need to reduce the sensitivity of the meter by setting the knob to the X10 range. Then measure the count rate as a function of the operating voltage.
Incorporate in your report an outline on the three nuclear decay mechanisms. The function of the GM counter should also be explained briefly in the report.
References
- Knoll, G.F., Radiation Detection and Measurement, 2nd ed.
- Tsoulfanidis, N., Measurement and Detection of Radiation.
- Rohlf, J.W., Modern Physics from α to Z0, Wiley 1994 https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/q36jf8/alma991011387139705164
- Thornton, Stephen T., and Andrew F. Rex. Modern Physics for Scientists and Engineers . 3rd ed. Belmont, CA: Thomson, Brooks/Cole, 2006. Print. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/q36jf8/alma991026442989705164
- Brehm J.J., Mullin, W.J. Modern Physics, Wiley 1989
- Taylor, J.R., An Introduction to Error Analysis, University Science Books, 1997.
- Cork, J.M., Radioactivity and Nuclear Physics, D. van Nostrand 195