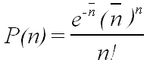Difference between revisions of "Main Page/PHYS 3220/Radioactive Decays"
| Line 58: | Line 58: | ||
<li>Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below). | <li>Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below). | ||
<table width=700 align=center> | <table width=700 align=center> | ||
| − | <tr><td | + | <tr><td>Number of Counts in interval (n)</td><td>No. of times Count occurs</td><td>''P(n)''</td><td>Total Counts</td></tr> |
<tr><td>0</td> <td>I(1)</td> <td>0.01</td> <td>0x1=0</td></tr> | <tr><td>0</td> <td>I(1)</td> <td>0.01</td> <td>0x1=0</td></tr> | ||
<tr><td>1</td> <td>II(2)</td> <td>0.03</td> <td>1x3=3</td></tr> | <tr><td>1</td> <td>II(2)</td> <td>0.03</td> <td>1x3=3</td></tr> | ||
<tr><td>2</td> <td>IIII I(5)</td> <td>0.05</td> <td>2x5=10</td></tr> | <tr><td>2</td> <td>IIII I(5)</td> <td>0.05</td> <td>2x5=10</td></tr> | ||
| − | <tr><td>etc..</td><td></td>td></td>td></td></tr> | + | <tr><td>etc..</td><td></td><td></td><td></td></tr> |
</table> | </table> | ||
</li> | </li> | ||
</ol> | </ol> | ||
Revision as of 10:21, 22 July 2011
Contents
Radioactive Decays
In this experiment a Geiger-Müller counter with a computer interface is used to detect the radiation coming from the natural background, as well as from some weak sources. The statistics of the decays is investigated to confirm the independence of the decay mechanism. The dependence of the count rate on the distance from the source is also investigated. Also, the Geiger-Müller method for detection of radioactivity will be investigated.
Introduction
Radioactive Decays
Radioactive nuclear decays can be classified according to their decay mechanism:
α-decay: heavy radionucleides often decay via the emission of a cluster composed of 2 protons and 2 neutrons, i.e., a 2He4 nucleus.
β-decay: nuclei away from the line of stability N = Z, where N is the total number of neutrons, and Z the total number of protons, can lower their energy, and hence become more stable by emitting either an electron or a positron. In the case of neutron-rich nuclei a fast electron is emitted from the nucleus, thus converting a neutron into a proton (and an electron + antineutrino) - corresponding to the β- decay of free neutrons (half-life 10.6 min.). For proton-rich nuclei a fast positron emerges from the nucleus (β+ decay) whereby a proton is converted into a neutron and a neutrino. This latter process may seem counterintuitive as it cannot occur for free protons (why?). The rest of the nuclear system supplies the energy necessary for the reaction to take place.
γ-decay: the emission of photons with higher energies than hard X-rays (MeV-range) is the result of a nuclear transition from an excited to a lower state in complete analogy with photon emission from excited atoms (eV to keV-range). This decay almost always accompanies α- and β-decays, since these processes usually leave the daughter nucleus in an excited state.
spontaneous fission:the emission of nuclear clusters bigger than α-particles is a rare process that has been studied recently in a systematic way at heavy ion facilities. It represents an alternative but rare decay mechanism, which provides insight into the nature of nuclear forces.
All modern physics texts contain a chapter that describes nuclear phenomenology as well as a table of isotopes. Understand the basic principles (there will be no need to understood previous chapters of the book for this!). See, e.g., refs. 1-3.
Detection of radiation
The detection of nuclear radiation relies on the property that it ionizes the surrounding matter through which it passes. This statement is obvious for the charged α, and β particles. For γ particles the ionization arises through the photoeffect and Compton scattering (ref. 1-3). This ionization can be detected through the electric spark induced between condenser plates that are biased with a high voltage, resulting in a short burst of current. This is the principle of a Geiger-Müller (GM) tube. The efficiency of detection depends on the voltage applied to the gas-filled tube (why can’t one use a vacuum tube?). It is important to realize that the detector has a finite efficiency, i.e., it does not detect every single α, β, or γ particle entering the detector. In particular, the efficiency depends on the voltage applied with a threshold behaviour (around 900 V) followed by saturation. In small hand-held radiation counters the high voltage is produced by a DC-DC converter as used in electronic flashlights. Read the description of GM counters available in many texts (e.g. ref. 1,2,6), and provide a concise description inyour own words with your report
Other detection mechanisms used for monitoring are: (i) exposure blackening of photographic film, e.g., in personal total dose monitors; (ii) scintillator counters; (iii) triggering of semiconductor devices; etc.
Absorption of radiation
Radiation is slowed down and eventually stopped by passage through matter. This is used both in shielding, as well as in applications of radiation for energy deposition (e.g., burning of cancer cells in radiation medicine). The absorption of the three different forms of radiation by matter is very different: α particles are heavy and, therefore, give up their energy readily in collisions with the nuclei of the surrounding matter; β particles are lighter and faster (as they emerge from the decay), and therefore pass more readily through matter until they are stopped. Gamma rays have the best penetration characteristics, i.e., are hardest to shield. α particles, which have typical energies of 5 MeV are stopped by a few centimeters of air, since they are doubly charged and slow compared to β particles. They are detected by GM counters only if they enter through an especially designed opening (transparent to them provided they are fast enough).
The stopping power and energy deposition is also a function that depends strongly on the kinetic energy of the ionizing particles. In radiation medicine this is used, e.g., by having fast particles penetrating healthy tissue with limited damage but sufficient slow-down, such that energy deposition becomes efficient when the tissue to be destroyed is reached. Usually physicists with nuclear medicine training are in charge of designing a radiation plan for each patient depending on the location of the tissue to be destroyed, vicinity of vital organs, etc. This is a non-trivial process, since secondary radiation (e.g., production of electrons) contributes to the energy deposition and may diffuse the flux of radiation. Read the detailed write-up for the “Absorption of Radiation” experiment.
Lifetimes of radioactive sources
A proper understanding of nuclear decays on the basis of a nuclear shell model (in analogy to atomic structure of electronic energy levels) enables one to predict the energies of the emitted particles as well as the half-lifes. The lifetime is related to the broadening in energy of the decaying state and can be understood from Heisenberg's uncertainty principle. (As a function of time the number of decaying particles is described by an exponential decay law.)
The radioactive sources that we use in this experiment do not permit a measurement of the decay law, since they have long lifetimes (tens to thousands of years), i.e., it is impossible to observe the decrease in radioactivity over a reasonable time span. However, sources with a short lifetime can be produced by exposure of a sample to a high-flux source, e.g., a reactor, which results in the conversion of stable nuclei into unstable ones.
Statistics of nuclear counting
In the early studies of radioactivity the question had to be resolved whether radioactivity was a purely random process, or whether the emission of one particle might effect the emission of others. One can prove that the observation of the number of independent decays per time interval (count rate) as a function of time should result in a Poissonian distribution (ref. 5). In the limit of high count rates the Poissonian distribution goes over into a Gaussian.
Rutherford performed experiments which showed that the probability, P(n), of observing n counts in a fixed time interval followed the Poisson formula
| (1) |
where the average number of counts per interval is calculated as
For all the measurements in this experiment that are performed with computerized data acquisition and data analysis, the Poissonian character of the statistical distribution of decay events are to be investigated and verified. Since the computer program Radiation Counter ***CHANGE THIS PROGRAM REFERENCE**** performs the statistical analysis automatically, it is crucial that you think through the steps involved in obtaining the histogram (cf.. also chapter 11 in ref. 5).
To illustrate how one explicitly analyzes the data we include an example for your convenience.
- Let us say that you record the number of counts heard during 100 five-second intervals by entering a mark in the column appropriate for that number of counts (col. 2 in the table below).
Number of Counts in interval (n) No. of times Count occurs P(n) Total Counts 0 I(1) 0.01 0x1=0 1 II(2) 0.03 1x3=3 2 IIII I(5) 0.05 2x5=10 etc..