Difference between revisions of "Main Page/PHYS 3220/Interferometer"
| Line 17: | Line 17: | ||
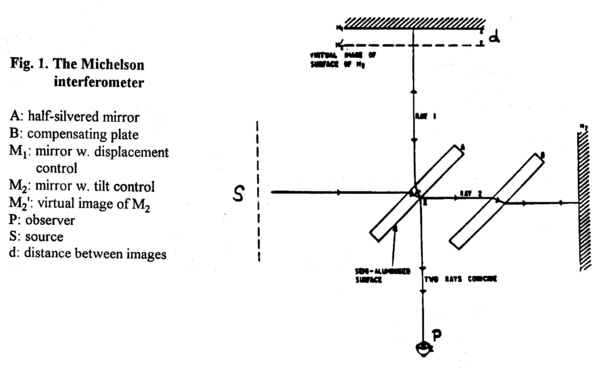
<p>In Fig. 1 the schematic diagram is shown for the M.I. with the semi-transparent mirror positioned at 45 degrees splitting the source beam into two halves that then travel toward the mirrors M<sub>1</sub> and M<sub>2</sub>. The electric field associated with a monochromatic planar wave with circular frequency ω=2πc/λ, and wavenumber k=2π/λ is given by</p> | <p>In Fig. 1 the schematic diagram is shown for the M.I. with the semi-transparent mirror positioned at 45 degrees splitting the source beam into two halves that then travel toward the mirrors M<sub>1</sub> and M<sub>2</sub>. The electric field associated with a monochromatic planar wave with circular frequency ω=2πc/λ, and wavenumber k=2π/λ is given by</p> | ||
| + | |||
| + | <table width=400 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mic-eqn1.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(1)</b></td></tr></table> | ||
| + | |||
| + | <p>The waves that are reflected at M1 and M2 are again split by the half-silvered mirror. We are interested in the signal arriving at P (the observer’s eye). Let M<sub>2</sub>' be the virtual image of M<sub>2</sub> as seen by P (along the line of sight of M<sub>1</sub>), and d be the separation between M<sub>1</sub> and M<sub>2</sub>'.The mirrors are carefully adjusted such that M<sub>1</sub> and M<sub>2</sub>' are parallel. The difference in path length of the light is thus given by 2''d''. The amplitudes of the two waves reaching the point P simultaneously are equal, and independent of the reflectivity of the half-silvered mirror (!), whereas their respective phases φ<sub>i</sub> are going to be different depending on the traversed path lengths. </p> | ||
| + | |||
| + | <table width=400 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mic-eqn2.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(2)</b></td></tr></table> | ||
| + | |||
| + | <p>From (1) it is obvious that the phase difference depends on the path length difference ''2d'' and on the wavelength of the monochromatic light:</p> | ||
| + | |||
| + | <table width=400 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mic-eqn3.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(3)</b></td></tr></table> | ||
| + | |||
| + | <p>The time-averaged intensity of the light I<sub>T</sub> observed at P is given by</p> | ||
| + | <table width=400 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mic-eqn4.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(4)</b></td></tr></table> | ||
| + | |||
| + | <p>Consequently the M.I. acts as a wavelength-dependent mirror, and depending on the phase difference φ , I<sub>T</sub> varies between 0 and the time-averaged incident intensity I<sub>0</sub>. </p> | ||
Revision as of 13:20, 22 July 2011
The Michelson Interferometer
In this experiment a Michelson interferometer is calibrated using a known mercury line, and then used to make a wavelength determination for the Na doublet. In addition, the index of refraction of a piece of plastic, and that of air at room pressure is determined.
Introduction
The Michelson interferometer is well known for the role it played in finding that the speed of light is the same in every reference frame, and thus to begin the development of the special theory of relativity. It is a simple set-up by means of a half-silvered and two ordinary mirrors to split a beam of light into two, allowing one beam to travel a different path length than the other in order to superimpose them. Small variations in the path length difference d allow us to observe the wave nature of light, i.e., to observe how the two beams can add to produce an interference pattern. An observation of the interference pattern as d is changed allows us to draw conclusions about the wavelength of coherent monochromatic light.
An interferometer is one of several instruments to demonstrate the wave nature of light (ref. 1). Other important two-beam experiments are, e.g., the Fresnel mirror, Young’s double-slit experiment, a thin film, or a grating (cf. the spectrometer used in Expt 9). A more sophisticated version of the interferometer used extensively in research is the Fabry-Perot interferometer. Use the references to understand how these interferometers work and what is meant by spatial and temporal coherence of light coming from an extended source.
|
Figure 1 - The Michelson Interferometer.
|
In Fig. 1 the schematic diagram is shown for the M.I. with the semi-transparent mirror positioned at 45 degrees splitting the source beam into two halves that then travel toward the mirrors M1 and M2. The electric field associated with a monochromatic planar wave with circular frequency ω=2πc/λ, and wavenumber k=2π/λ is given by
| (1) |
The waves that are reflected at M1 and M2 are again split by the half-silvered mirror. We are interested in the signal arriving at P (the observer’s eye). Let M2' be the virtual image of M2 as seen by P (along the line of sight of M1), and d be the separation between M1 and M2'.The mirrors are carefully adjusted such that M1 and M2' are parallel. The difference in path length of the light is thus given by 2d. The amplitudes of the two waves reaching the point P simultaneously are equal, and independent of the reflectivity of the half-silvered mirror (!), whereas their respective phases φi are going to be different depending on the traversed path lengths.
| (2) |
From (1) it is obvious that the phase difference depends on the path length difference 2d and on the wavelength of the monochromatic light:
| (3) |
The time-averaged intensity of the light IT observed at P is given by
| (4) |
Consequently the M.I. acts as a wavelength-dependent mirror, and depending on the phase difference φ , IT varies between 0 and the time-averaged incident intensity I0.