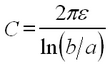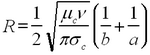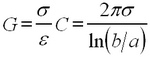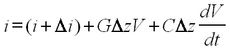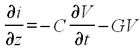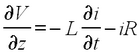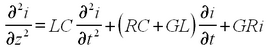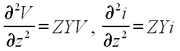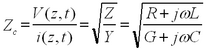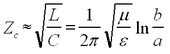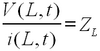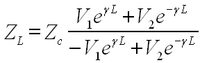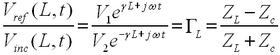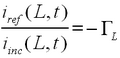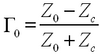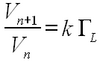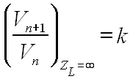Difference between revisions of "Main Page/PHYS 4210/Coaxial Cable"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<h1>Coaxial Cable</h1> | <h1>Coaxial Cable</h1> | ||
| − | <p> | + | <p>Carefully read Experiment 1 in The Art of Experimental Physics, Preston and Dietz, [[Media:Coaxial-AEP-1991.pdf|available here]]<ref>[https://www.library.yorku.ca/find/Record/1038893 The Art of Experimental Physics], John Wiley and Sons,1991.</ref>. This write-up is meant to supplement that material. |
| + | </p> | ||
<h2>Key Concepts</h2> | <h2>Key Concepts</h2> | ||
| Line 235: | Line 236: | ||
<h1>References</h1> | <h1>References</h1> | ||
| − | < | + | <references/> |
| − | < | + | |
| − | + | <p> 2. J.M. Serra ''et. al.'', "''A wave lab inside a coaxial cable''", [http://ajp.aapt.org/resource/1/ajpias/v55/i4/p366_s1 Eur. J. Phys. '''25''' (2004) 581]</p> | |
| − | |||
Latest revision as of 13:52, 15 January 2021
Contents
Coaxial Cable
Carefully read Experiment 1 in The Art of Experimental Physics, Preston and Dietz, available here[1]. This write-up is meant to supplement that material.
Key Concepts
|
|
Theory
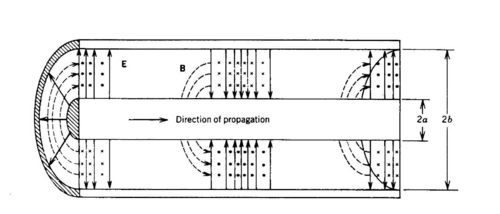
A coaxial cable (coax) is one of the most popular means for transmitting the electromagnetic power from a generator to a receiver. It consists of an inner and outer conducting lines (usually made of copper) separated by a dielectric layer (usually teflon). The electromagnetic wave can propagate in a coax in the form of TE, TM, and TEM modes, and the latter is the one that is most commonly used. In this experiment, the effect of a coaxial cable on the propagating signal and some physical characteristics of a coax are studied.
There are two levels of description of electromagnetic phenomena. The more fundamental one relies on Maxwell’s equations combined with material equations. Within this approach, one uses the language of electric and magnetic field strengths, potentials, dielectric susceptibility and magnetic permeability, etc. Engineers, however, prefer a simpler language of currents, voltages and lump elements, that is, resistance, capacitance, conductance, and inductance. In order for this simplified description to be applicable to the problem considered, the characteristic sizes of lump elements must be much smaller than the wavelength of an electromagnetic wave. Nevertheless, with a small modification, the approach of engineers allows us to obtain some meaningful results even when this requirement is not met. We will adopt the language of engineers in the following discussion.
The idea of the modification is that, instead of using the net inductance, capacitance, resistance and conductance, we use their values per unit length. Thus, a coax is viewed as a system with distributed parameters. Let us write down the expressions for the unit-length characteristics of a coax. A current in the central conductor sets up a magnetic field; hence, the line has inductance whose value per unit length is
| (1) |
where μ is magnetic permeability of the dielectric layer between the two conductors, and a and b are the radii of the inner and outer conductors, respectively.
Next, the capacitance per unit length between the two conductors is:
| (2) |
where ε is the dielectric permittivity of the dielectric layer.
Since both inner and outer conductors are not ideal, the line has a resistance per unit length
| (3) |
Here, μc and σc are the magnetic permeability and conductivity of the conductors, respectively. The resistance value (3) is determined by the skin depth that measures the characteristic distance of penetration of the electromagnetic wave into the conductors. It is within the skin layer that the absorption of the electromagnetic power is most intense. The skin depth, in turn, depends on the frequency, ν, of the wave, hence R depends on ν as well.
Finally, the dielectric separating the two conductors is not ideal, hence there always is a leakage current when the conductors are kept at different potentials. This effect is accounted for by introducing the conductance per unit length of the line
| (4) |
σ being the conductivity of the dielectric layer.
Exercise: Derive (1) and (2). Hint: to derive (1), suppose that some current J flows through the inner conductor of the line. Find the value of the magnetic field produced by this current, and then the magnetic field energy stored in a unit length element of the line. This energy also equals LJ2/2, from the definition of inductance per unit length. To derive (2), assume that the inner and outer conductors have charges per unit length equal to +q and –q. Find the potential difference between the two conductors. From the definition of a unit length capacitance, the potential difference equals to q/C.
A coax can be thought of as a collection of infinitely many infinitesimal elements, each of which can be presented with an equivalent circuit shown in Fig. 1 (similar to Fig. 1.4 of Preston).
|
Figure 1 - Coaxial cable cross sectional view.
|
As the current travels along the inner conductor, its total decrease on the element Δz is the sum of the leakage currents through the capacitance and displacement current. The former equals to GΔzV , and the latter to CΔz(dV/dt). Considering the node that joins the inductance, conductance, and capacitance, the first Kirchoff’s law yields:
| (5) |
Rearranging the terms and taking the limit Δz → 0 , we obtain
| (6) |
Similarly, a voltage drop on this element equals the electromotive force of self-induction and the voltage developed across the resistance:
| (7) |
Exercise: Derive (7). Use the second Kirchoff’s law to find the voltage drop across Δz.
Differentiating the last two equations with respect to z, we obtain:
| (8) |
| (9) |
Exercise: Show this.
These equations are called telegraph equations. We will look for their solution in the harmonic form
| (10) |
Substitution of these expressions into the original telegraph equations (8) yields:
| (11) |
where the total series impedance and shunt conductance are
| (12) |
Equations (11) and (12) allow solutions in the form
| (13) |
where
| (14) |
is the propagation constant. It is a complex number whose real part, α, is called attenuation constant, and the imaginary part, β, is the phase constant. The two terms in Eqs. (13) represent the waves travelling in the positive and negative z-directions.
Exercise: Which one is which? Hint: The wave attenuates in the direction of propagation.
Since the telegraph equations for voltage and current are of the same form, it can be concluded that the relationship between the amplitudes of currents and voltages propagating to the right and to the left is linear. The proportionality constant relating these quantities is called the characteristic impedance of the line, and its value equals to
| (15) |
as can be verified from Eqs.(6, 7). It then follows that
| (16) |
In the high-frequency limit,ωL >> R, ωC >> G (or, alternatively, for an ideal line with perfect inner and outer conductors and a perfectly insulating dielectric layer in between), the expression for the characteristic impedance of the line simplifies to
| (17) |
Note that the characteristic impedance of an ideal line is a frequency-independent quantity whose imaginary part equals to zero.
Exercise: Derive the expression for Zc. Hint: Use Eq. (6) or (7) to find the relationship between current and voltage amplitudes from the general solution (13).
Suppose that one end of the line is terminated at z = L with a load of impedance ZL, so that the relationship between current and voltage on the load is
| (18) |
Substitution of Eqs. (16) for currents yields:
| (19) |
The amplitudes V1 and V2 can be interpreted as the amplitudes of the waves reflected from and incident on the load, respectively. It then follows that the ratio of the reflected to incident voltage at z = L, called reflection coefficient from the output, is:
| (20) |
For currents,
| (21) |
Exercise: Why?
It is evident from Eq. (20) that ΓL changes from +1 (open end, ZL = ∞) to –1 (shorted, ZL = 0), depending on the value of load impedance. Impedance matching of the load to the line occurs when ZL = Zc. In this case, ΓL = 0 and there is no reflected wave.
Let us finally recall that the generator itself has a finite input impedance Z0. Redefining the voltage amplitudes V1 and V2 as those of the waves incident on and reflected from the input, we find the input reflection coefficient
| (22) |
Again, input impedance matching occurs when Z0 = Zc and Γ0 = 0.
Experiment
In this experiment, the following equipment will be used:
- A coaxial cable of 20 to 30 m in length
- Rectangular pulse generator
- Oscilloscope
- Differentiating RC-circuit
- Multimeter
- Adjustable resistor
Part 1
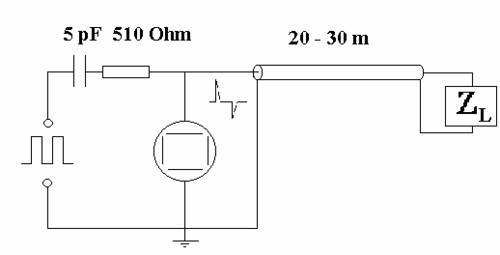
Connect the circuit as shown in Fig. 2. Rectangular pulses produced by the generator are differentiated by the RC-circuit, so that voltage entering the coaxial line represents a series of spikes, as shown in the figure. Set the generator frequency to 10 kHz. With infinite resistance of the load, observe the multireflected pulse on the oscilloscope. Explain the shape of the observed signal. Next, connect the inner and outer conductors of the line at the output end with a wire. Explain the difference of the observed multireflected pulse from the previous case. With ZL= ∞ , calculate the velocity of pulse propagation along the line. Determine the dielectric constant of teflon from the measured velocity. Use the vacuum value for the magnetic permeability of teflon, μ=4πx10-7 NA-2.
|
Figure 2 - Circuit to study pulses propagating along the line.
|
Measure directly the capacitance of the coax with a multimeter. Determine the dielectric constant and compare it to the previously obtained value. Comment on the possible discrepancy.
Part 2
Assuming the ideal line, calculate its characteristic impedance from Eq. (17). Again, use the vacuum value for the magnetic permeability of teflon.
Attach a variable resistance to the output end of the line and measure the reflection coefficient at the output as a function of load resistance. The following procedure is suggested.
First, reconnect the circuit as shown in Fig. 2 and turn on the generator to produce the multireflected pulse. The heights of the nth and (n+1)th spikes are related to each other as:
| (23) |
Exercise: What is the proportionality constant k equal to in terms of the attenuation constant and the input reflection coefficient?
At each value of ZL, choose two consecutive spikes and measure the ratio of their heights. Note that the first and the second spikes are not a very good choice because the first pulse coming directly from the generator via the differentiating circuit gets absorbed not only in the coaxial line, but also in various connections between the coax, the differentiator, and the scope. Feel free to adjust the generator frequency and oscilloscope settings to get an optimal scope trace. In order to find the proportionality constant k in (23), you can use the fact that at infinite load resistance (open output end of the line), the coefficient of reflection at the output equals one:
| (24) |
Plot ΓL vs. ZL. Fit this plot with Eq. (20) to determine the characteristic impedance of the line. Does this value of Zc agree with your previously obtained estimate?
Part 3
With the circuit connected as in Fig. 2, determine the line’s attenuation constant from the observed multireflected pulse. Is it safe to assume that the input reflection coefficient equals one? Justify this assumption experimentally and theoretically by estimating the input reflection coefficient. Note that the impedance of the scope is about 1 MΩ, and the typical impedance of the generator is 600 Ω. Assume for simplicity that the capacitance has zero resistance.
References
- ↑ The Art of Experimental Physics, John Wiley and Sons,1991.
2. J.M. Serra et. al., "A wave lab inside a coaxial cable", Eur. J. Phys. 25 (2004) 581