Difference between revisions of "Main Page/PHYS 3220/new Excitation Potentials"
| (8 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
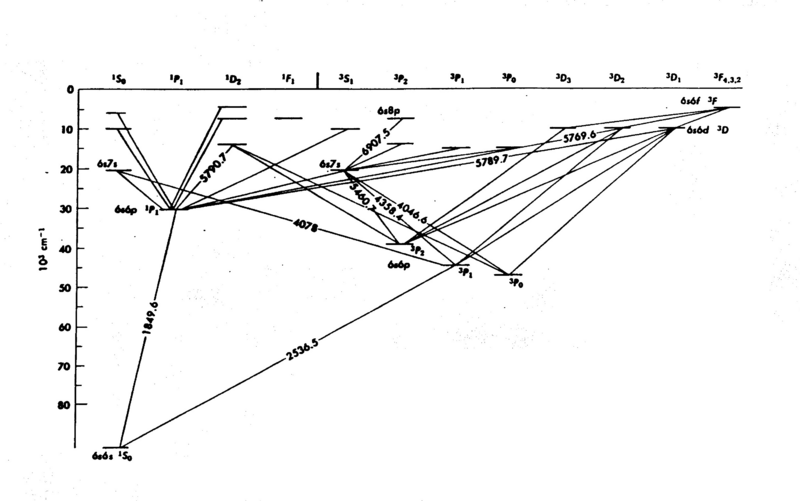
<p>The energy levels of mercury (Hg) are shown in Fig. 1; it is easy to see that the internal structure is complicated - a consequence of the many electrons in the atom. The diagram gives considerable information you need to know for this experiment. The numbers associated with the lines drawn between the energy levels are wavelengths (in Angstroms Å). In the present experiment we explore only the energy levels 6<sup>3</sup>P on the diagram, the first group of excited states. The electrons do not acquire enough energy to excite many of the other levels.</p> | <p>The energy levels of mercury (Hg) are shown in Fig. 1; it is easy to see that the internal structure is complicated - a consequence of the many electrons in the atom. The diagram gives considerable information you need to know for this experiment. The numbers associated with the lines drawn between the energy levels are wavelengths (in Angstroms Å). In the present experiment we explore only the energy levels 6<sup>3</sup>P on the diagram, the first group of excited states. The electrons do not acquire enough energy to excite many of the other levels.</p> | ||
<p>The Franck-Hertz apparatus consists of an evacuated glass envelope containing a cathode, screen, plate and a small drop of mercury, which can be vaporized by heating. The plate is always kept slightly negative with respect to the grid (that acts as an anode, i.e. accelerates the electrons) and both are set at various positive voltages with respect to the cathode. As the grid potential is raised, the plate current increases accordingly. For accelerating voltages below 5V all collisions with mercury atoms will be elastic (kinetic energy below about 5 eV). Hence, these electrons are energetic enough to overcome the negative plate-grid potential and are collected by the plate. The current flowing in the tube depends upon both the number of charged carriers (electrons) and their velocities (j = nev). Thus a significant change in the particle velocity can affect the size of the current. Once electrons with more than about 5eV energy excite a mercury atom, they slow down and the current flowing in the tube drops. If there is a larger voltage across the tube so that the electron can be re-accelerated to ~ 5 eV after giving it up once in the first collision, then we can see decreases in the current at higher voltages corresponding to a repeated inelastic collision. This process can yield a cyclic rise and fall of the current with the voltage.</p> | <p>The Franck-Hertz apparatus consists of an evacuated glass envelope containing a cathode, screen, plate and a small drop of mercury, which can be vaporized by heating. The plate is always kept slightly negative with respect to the grid (that acts as an anode, i.e. accelerates the electrons) and both are set at various positive voltages with respect to the cathode. As the grid potential is raised, the plate current increases accordingly. For accelerating voltages below 5V all collisions with mercury atoms will be elastic (kinetic energy below about 5 eV). Hence, these electrons are energetic enough to overcome the negative plate-grid potential and are collected by the plate. The current flowing in the tube depends upon both the number of charged carriers (electrons) and their velocities (j = nev). Thus a significant change in the particle velocity can affect the size of the current. Once electrons with more than about 5eV energy excite a mercury atom, they slow down and the current flowing in the tube drops. If there is a larger voltage across the tube so that the electron can be re-accelerated to ~ 5 eV after giving it up once in the first collision, then we can see decreases in the current at higher voltages corresponding to a repeated inelastic collision. This process can yield a cyclic rise and fall of the current with the voltage.</p> | ||
| + | |||
| + | <table width=400 align=center><td> | ||
| + | <p align=justify>[[File:Fh-fig1.png|800px|border|center]] | ||
| + | <b>Figure 1 -</b> Energy Levels of Mercury. | ||
| + | <br clear=right> | ||
| + | </p> | ||
| + | </td></table> | ||
<h1>Procedure</h1> | <h1>Procedure</h1> | ||
| Line 12: | Line 19: | ||
<h2>Required Components</h2> | <h2>Required Components</h2> | ||
| − | <p> For this experiment you will be using equipment provided by Leybold®. Go to https://www.leybold-shop.com/physics/physics-equipment/atomic-and-nuclear-physics/franck-hertz-experiments/mercury/franck-hertz-supply-unit-555880.html and click on <b>Related Documents</b>. Read through sections 1-4, 5.1, 5.2 and 5.6 | + | <p> For this experiment you will be using equipment provided by Leybold®. Go to https://www.leybold-shop.com/physics/physics-equipment/atomic-and-nuclear-physics/franck-hertz-experiments/mercury/franck-hertz-supply-unit-555880.html and click on <b>Related Documents</b>. Read through the instruction sheet for the Franck-Hertz Supply Unit (pay attention to sections 1-4, 5.1, 5.2 and 5.6) and the Experiment Descriptions for Hg (P6.2.4.1) and Ne (P6.2.4.3). These leaflets provide useful information on how to use the equipment and optimize the Franck-Hertz signal. THE EXPERIMENTAL SETUP OF THE TEMPERATURE PROBE IS CRITICAL - THE PROBE MUST BE INSERTED INTO THE BLIND HOLE OF THE COPPER TUBE of the oven. Ensure the temperature sensor is properly connected and IS NOT TOUCHING THE Hg Franck-Hertz tube. </p> |
<h3>Observing the Signal</h3> | <h3>Observing the Signal</h3> | ||
| Line 18: | Line 25: | ||
<p>Electrons liberated from the filament and accelerated to the detector plate which do not collide with an Hg atom will register as a current. This current is amplified by the supply unit and be viewed on the oscilloscope. Note that evidence of collisions with Hg atoms will result in a deficit of current at specific accelerating voltages. This will be observed as dips on the oscilloscope trace. It is the origin and properties of these dips which is the focus of this experiment.</p> | <p>Electrons liberated from the filament and accelerated to the detector plate which do not collide with an Hg atom will register as a current. This current is amplified by the supply unit and be viewed on the oscilloscope. Note that evidence of collisions with Hg atoms will result in a deficit of current at specific accelerating voltages. This will be observed as dips on the oscilloscope trace. It is the origin and properties of these dips which is the focus of this experiment.</p> | ||
| − | <p>When the temperature is stable you can record the current-voltage characteristic of the Franck-Hertz tube. The current-voltage trace can be | + | <p>When the temperature is stable you can record the current-voltage characteristic of the Franck-Hertz tube. The current-voltage trace can be observed using the oscilloscope in XY mode. Make sure the signal you observe does not have horizontal clipping (the peaks cut off); see the leaflets for guidance on how to optimize your signal. (What is the meaning of the vertical cut-off?)</p> |
| − | <p>Record an I-V curve for an initial temperature of about 180ºC . | + | <p>Record an I-V curve for an initial temperature of about 180ºC. Set the oscilloscope display mode to XY and the persist to 2 seconds to best visually observe the oscilloscope signal on the screen. </p> |
<h3>Saving the Scope Traces</h3> | <h3>Saving the Scope Traces</h3> | ||
| − | <p> | + | <p>Use a USB to save your optimized Franck-Hertz signals using the following procedure. (For more information on saving in XY mode refer to the user manual for the oscilloscope.) </p> |
<ol> | <ol> | ||
| − | <li> | + | <li>Connect your USB device to the oscilloscope. </li> |
| − | <li> | + | <li>Switch the oscilloscope display mode from XY to YT.</li> |
| − | <li> | + | <li>Push the Save/Recall button on the oscilloscope to activate the save menu. </li> |
| − | <li> | + | <li>Push the "Print" button to save all files to your USB drive. (The "Print" button is set to "Save All Files". This will save waveforms on Ch.1 and Ch.2 and a picture of the waveforms. </li> |
| − | |||
| − | |||
</ol> | </ol> | ||
| + | |||
<h2>Measurements</h2> | <h2>Measurements</h2> | ||
| − | <p>Find as many values as you can of the excitation energy ("excitation potential") from your record. Repeat these measurements for | + | |
| + | <p>Find as many values as you can of the excitation energy ("excitation potential") for Hg from your record. Repeat these measurements for 5 different temperature values ranging from 140ºC to 195ºC. <b>DO NOT EXCEED a setpoint temperature of 195ºC on the supply unit.</b> Comment on the effect of the Hg pressure in the tube. Perform a full error analysis and compare your results with the expected values.</p> | ||
| + | <p> The neon tube is operated at room temperature. Optimize and record the Ne Franck-Hertz curve and find the excitation energy values for Ne. Compare with the expected values. Can you see the luminous layers in the neon tube? (Hint: Use the MAN operating mode to manually adjust the accelerating voltage and turn off the lights in the room.) | ||
<h1>Questions</h1> | <h1>Questions</h1> | ||
<ol> | <ol> | ||
| − | |||
| − | |||
<li>Explain the effect of changing the grid-to-plate voltage (V<sub>1</sub>)?</li> | <li>Explain the effect of changing the grid-to-plate voltage (V<sub>1</sub>)?</li> | ||
| − | |||
<li>Find out what is meant by "contact potential" in the Franck-Hertz tube and explain how it could be determined. Can you estimate it from your record?</li> | <li>Find out what is meant by "contact potential" in the Franck-Hertz tube and explain how it could be determined. Can you estimate it from your record?</li> | ||
| − | + | <li>Determine from simple classical mechanics (using a head-on collision with recoil at 180 degrees) what fraction of an electron's kinetic energy can be transferred to a mercury atom in an '''elastic''' collision. Derive an approximate value of the fraction. Repeat for a neon atom. </li> | |
| − | <li>Determine from simple classical mechanics (using a head-on collision with recoil at 180 degrees) what fraction of an electron's kinetic energy can be transferred to a mercury atom in an '''elastic''' collision. Derive an approximate value of the fraction.</li> | ||
| − | |||
<li>Why are the other levels not observed? (e.g. 6<sup>3</sup>P<sub>2</sub>, 6<sup>3</sup>P<sub>o</sub>, 6<sup>1</sup>P<sub>1</sub>.)</li> | <li>Why are the other levels not observed? (e.g. 6<sup>3</sup>P<sub>2</sub>, 6<sup>3</sup>P<sub>o</sub>, 6<sup>1</sup>P<sub>1</sub>.)</li> | ||
</ol> | </ol> | ||
| Line 54: | Line 57: | ||
<li>Brehm, J., Mullin W, ''Modern Physics'', p. 168</li> | <li>Brehm, J., Mullin W, ''Modern Physics'', p. 168</li> | ||
<li>Halliday, D., Resnick, R., ''Physics I'', pp. 522-24.</li> | <li>Halliday, D., Resnick, R., ''Physics I'', pp. 522-24.</li> | ||
| − | <li>Carpenter, K.H., [http://ajp.aapt.org/resource/1/ajpias/v43/i2/p190_s1| Amer. J. Phys. '''43''' (1975) 190].</li> | + | <!-- <li>Carpenter, K.H., [http://ajp.aapt.org/resource/1/ajpias/v43/i2/p190_s1| Amer. J. Phys. '''43''' (1975) 190].</li> --> |
| − | <li>Hanne, G.F. | + | <li>Hanne, G. F. “What Really Happens in the Franck–Hertz Experiment with Mercury?” American journal of physics 56.8 (1988): 696–700. Web. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_scitation_primary_10_1119_1_15503 </li> |
| − | <li> | + | <li>Huebner, J. S. “Comment on the Franck–Hertz Experiment.” American journal of physics 44.3 (1976): 302–303. Web. |
| − | <li>Liu, F.H. | + | https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_crossref_primary_10_1119_1_10596</li> |
| + | <li>Liu, F. H. “Franck–Hertz Experiment with Higher Excitation Level Measurements.” American journal of physics 55.4 (1987): 366–369. Web. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_crossref_primary_10_1119_1_15174</li> | ||
<li>Preston, D., Dietz, E.,'' The Art of Experimental Physics'', pp. 197ff.</li> | <li>Preston, D., Dietz, E.,'' The Art of Experimental Physics'', pp. 197ff.</li> | ||
</ol> | </ol> | ||
Latest revision as of 13:20, 13 August 2021
Contents
The Franck-Hertz Experiment: Excitation Potentials of Mercury and Neon
Introduction
One of the most direct proofs of the existence of discrete energy states within the atom was first demonstrated in experiments on critical potentials, performed initially by Franck and Hertz in the early 1900's. Studying the way electrons lose energy in collisions with mercury vapour, they laid the basis for the quantum theory of atoms by observing that the electrons give energy to internal motion of mercury atoms in discrete units only.
The collision of a neutral atom with a fast particle (e.g., an electron) may result in the excitation or ionization of the atom. A slow electron in an elastic collision can give very little of its kinetic energy to the translational motion of a mercury atom (without changing the energy state of the atom) - just as a ping-pong ball cannot effectively move a billiard ball. If a moderately slow electron has enough kinetic energy to overcome an atomic excitation threshold (several eV) the collision may be inelastic and much of the energy of the electron can go into exciting a higher state of the atom. The energy in electron volts (eV) necessary to raise an atom from its normal ("ground") state to a given excited state is called the excitation potential for that state. For sufficiently high scattering energy of the impinging electron even ionization may occur.
The energy levels of mercury (Hg) are shown in Fig. 1; it is easy to see that the internal structure is complicated - a consequence of the many electrons in the atom. The diagram gives considerable information you need to know for this experiment. The numbers associated with the lines drawn between the energy levels are wavelengths (in Angstroms Å). In the present experiment we explore only the energy levels 63P on the diagram, the first group of excited states. The electrons do not acquire enough energy to excite many of the other levels.
The Franck-Hertz apparatus consists of an evacuated glass envelope containing a cathode, screen, plate and a small drop of mercury, which can be vaporized by heating. The plate is always kept slightly negative with respect to the grid (that acts as an anode, i.e. accelerates the electrons) and both are set at various positive voltages with respect to the cathode. As the grid potential is raised, the plate current increases accordingly. For accelerating voltages below 5V all collisions with mercury atoms will be elastic (kinetic energy below about 5 eV). Hence, these electrons are energetic enough to overcome the negative plate-grid potential and are collected by the plate. The current flowing in the tube depends upon both the number of charged carriers (electrons) and their velocities (j = nev). Thus a significant change in the particle velocity can affect the size of the current. Once electrons with more than about 5eV energy excite a mercury atom, they slow down and the current flowing in the tube drops. If there is a larger voltage across the tube so that the electron can be re-accelerated to ~ 5 eV after giving it up once in the first collision, then we can see decreases in the current at higher voltages corresponding to a repeated inelastic collision. This process can yield a cyclic rise and fall of the current with the voltage.
|
Figure 1 - Energy Levels of Mercury.
|
Procedure
Required Components
For this experiment you will be using equipment provided by Leybold®. Go to https://www.leybold-shop.com/physics/physics-equipment/atomic-and-nuclear-physics/franck-hertz-experiments/mercury/franck-hertz-supply-unit-555880.html and click on Related Documents. Read through the instruction sheet for the Franck-Hertz Supply Unit (pay attention to sections 1-4, 5.1, 5.2 and 5.6) and the Experiment Descriptions for Hg (P6.2.4.1) and Ne (P6.2.4.3). These leaflets provide useful information on how to use the equipment and optimize the Franck-Hertz signal. THE EXPERIMENTAL SETUP OF THE TEMPERATURE PROBE IS CRITICAL - THE PROBE MUST BE INSERTED INTO THE BLIND HOLE OF THE COPPER TUBE of the oven. Ensure the temperature sensor is properly connected and IS NOT TOUCHING THE Hg Franck-Hertz tube.
Observing the Signal
Electrons liberated from the filament and accelerated to the detector plate which do not collide with an Hg atom will register as a current. This current is amplified by the supply unit and be viewed on the oscilloscope. Note that evidence of collisions with Hg atoms will result in a deficit of current at specific accelerating voltages. This will be observed as dips on the oscilloscope trace. It is the origin and properties of these dips which is the focus of this experiment.
When the temperature is stable you can record the current-voltage characteristic of the Franck-Hertz tube. The current-voltage trace can be observed using the oscilloscope in XY mode. Make sure the signal you observe does not have horizontal clipping (the peaks cut off); see the leaflets for guidance on how to optimize your signal. (What is the meaning of the vertical cut-off?)
Record an I-V curve for an initial temperature of about 180ºC. Set the oscilloscope display mode to XY and the persist to 2 seconds to best visually observe the oscilloscope signal on the screen.
Saving the Scope Traces
Use a USB to save your optimized Franck-Hertz signals using the following procedure. (For more information on saving in XY mode refer to the user manual for the oscilloscope.)
- Connect your USB device to the oscilloscope.
- Switch the oscilloscope display mode from XY to YT.
- Push the Save/Recall button on the oscilloscope to activate the save menu.
- Push the "Print" button to save all files to your USB drive. (The "Print" button is set to "Save All Files". This will save waveforms on Ch.1 and Ch.2 and a picture of the waveforms.
Measurements
Find as many values as you can of the excitation energy ("excitation potential") for Hg from your record. Repeat these measurements for 5 different temperature values ranging from 140ºC to 195ºC. DO NOT EXCEED a setpoint temperature of 195ºC on the supply unit. Comment on the effect of the Hg pressure in the tube. Perform a full error analysis and compare your results with the expected values.
The neon tube is operated at room temperature. Optimize and record the Ne Franck-Hertz curve and find the excitation energy values for Ne. Compare with the expected values. Can you see the luminous layers in the neon tube? (Hint: Use the MAN operating mode to manually adjust the accelerating voltage and turn off the lights in the room.)
Questions
- Explain the effect of changing the grid-to-plate voltage (V1)?
- Find out what is meant by "contact potential" in the Franck-Hertz tube and explain how it could be determined. Can you estimate it from your record?
- Determine from simple classical mechanics (using a head-on collision with recoil at 180 degrees) what fraction of an electron's kinetic energy can be transferred to a mercury atom in an elastic collision. Derive an approximate value of the fraction. Repeat for a neon atom.
- Why are the other levels not observed? (e.g. 63P2, 63Po, 61P1.)
References
- Brehm, J., Mullin W, Modern Physics, p. 168
- Halliday, D., Resnick, R., Physics I, pp. 522-24.
- Hanne, G. F. “What Really Happens in the Franck–Hertz Experiment with Mercury?” American journal of physics 56.8 (1988): 696–700. Web. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_scitation_primary_10_1119_1_15503
- Huebner, J. S. “Comment on the Franck–Hertz Experiment.” American journal of physics 44.3 (1976): 302–303. Web. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_crossref_primary_10_1119_1_10596
- Liu, F. H. “Franck–Hertz Experiment with Higher Excitation Level Measurements.” American journal of physics 55.4 (1987): 366–369. Web. https://ocul-yor.primo.exlibrisgroup.com/permalink/01OCUL_YOR/sqt9v/cdi_crossref_primary_10_1119_1_15174
- Preston, D., Dietz, E., The Art of Experimental Physics, pp. 197ff.