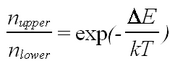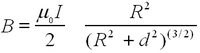Difference between revisions of "Main Page/PHYS 4210/Electron Spin Resonance"
| (One intermediate revision by the same user not shown) | |||
| Line 89: | Line 89: | ||
<h1>Procedure</h1> | <h1>Procedure</h1> | ||
| − | <p>To | + | <p>To prepare for the experimental setup read through [[Media:514571e.pdf|ESR Control Unit]], [[Media:P6262_e.pdf|Electron spin resonance at DPPH]] and [[Media:P6263_e.pdf|Passive RF Oscillator]]. |
<h2>Part I: Verify the detection technique for the resonance condition. </h2> | <h2>Part I: Verify the detection technique for the resonance condition. </h2> | ||
Latest revision as of 13:16, 15 January 2021
Electron Spin Resonance
The objective of this experiment is to investigate the electron's internal angular momentum called spin. A sample containing a substance with a 'free' electron in an s-state is placed in a homogeneous magnetic field of strength B, which splits the energy levels for electrons with spin projections aligned with the field compared to the counter-aligned ones. A radio-frequency generator is used to resonantly pump electrons from the spin state with lower energy to the upper state. Tracing the resonance as a function of B provides the means for determining the gyro-magnetic ratio of the electron.
Key Concepts
|
|
Introduction
In this experiment we obtain direct evidence for the unusual property of electrons, namely that while being point particles they exhibit the property of having two spin states. Most introductory texts on modern physics contain discussions of the historical developments leading to the discovery of this intrinsic angular momentum variable by Goudsmit and Uhlenbeck. Today we know that all elementary particles are spin - 1/2 objects called fermions, while the mediators of interactions are spin-1 objects called bosons (photons, gluons, W and Z gauge bosons for weak interactions). This experiment is also related to the study of electronic structure in magnetic and disordered systems; the 1977 Nobel Prize in physics went to P.W. Anderson, N.F. Mott, and J.H. Van Vleck for a number of achievements in this area. In chemistry ESR is applied as an important analysis technique to determine the properties of outer electrons responsible for covalent bonding in molecules. The twin concept to ESR is NMR - nuclear magnetic resonance - a technique known commonly as a non-intrusive medical diagnostic tool: it detects proton densities via their spin. It is also closely related to FMR – ferromagnetic resonance, and the Zeeman effect.
ESR is also known as EPR – electron paramagnetic resonance, since it deals only with paramagnetic materials. The atoms in a paramagnetic material have unpaired electrons, and therefore a net magnetic moment, but the internal interactions are not strong enough and do not create areas of similarly oriented magnetic moments, or ferromagnetism. The paramagnetic material is therefore a collection of randomly directed magnetic moments, all of which align the same direction due to the torque created by an external magnetic field. The paramagnetic material used in this experiment is an organic chemical called a free radical: diphnyl picryl hydrazyl (DPPH). The outer shell electron of this substance acts as though it was free, or almost so, resulting in a g-factor of 2.0023, which has a fractional difference of less than one part in a thousand from a perfectly free electron .
The idea in the spin resonance experiment is the following: if we place a macroscopic sample of material containing appropriate electrons in the vicinity of a radiating antenna, while an external magnetic field is present to make the energy splitting of the spin-up and spin-down states coincide with the energy of the radio wave quanta, we should be able to observe the fact that energy gets absorbed by the electrons in the sample. This observation is possible by detecting a change in a receiver placed in the vicinity, but also by observing the current that the radio generator passes through the coil (which acts as the antenna). In the microwave case one uses the former technique, while in the radiofrequency case (our experiment) the latter is preferred. The presence of the sample with resonating electrons (electrons in spin states of lower energy get transferred to the less favourable state, and decay later spontaneously) leads not only to a measurable change in the DC current through the coil, but also to a detuning of the frequency (the inductivity of the coil changes). For a discussion of both the radio wave and microwave methods read the descriptions of nuclear magnetic resonance and electron spin resonance in [1].
According to Quantum theory, an electron has ‘spin’, a property which behaves like angular motion, resulting in an angular momentum and consequently, as any ‘moving’ charge, a magnetic moment:
| (1) |
where µB is the Bohr magneton and g is the Landé factor. But since quantum theory permits only two values for the spin Sz= ± hbar/2 , the magnetic moment results in only two possible projections:
| (2) |
and the resulting energy levels are then:
| (3) |
Since the coupling of a magnetic moment with an external magnetic field B results in a torque aligning the magnetic moment with the field. The application of electromagnetic radiation to such a system, with a carefully set energy to match the splitting between the + and – values, results in the absorption of energy from the field, which is observable and therefore of interest to us:
| (4) |
here ω is the frequency of the applied electromagnetic field (What is the expected energy scale?). Since this result is for only a single free electron, while we’re dealing with a macroscopic sample, a statistical correction has to be made. Using the Boltzmann distribution for the energy levels N+ and N-:
| (5) |
where k is the Boltzmann constant and T is the temperature. It is important to note that a long natural lifetime of the upper state in a magnetic field is shortened at room temperature (kT=0.025eV), resulting in an equilibration of the spin level populations in a fraction of a second.
For most transition lines a fractional value of g was observed, a phenomenon highly important for the development of quantum theory. To unravel the complicated behavior of fractional g values in atomic spectroscopy, physicists had to figure out (before the advent of modern quantum mechanics) that the electron must have an internal angular momentum with an unusual value of g=2 (all classical charge distributions have g=1), and that this internal angular momentum when coupled to the orbital angular momentum (which has the classical value of g=1) leads to fractional g values for most optical transitions. Thus quantum mechanics was subject to tough testing with the Schrödinger-Pauli theory incorporating spin in an ad-hoc way, and explaining atomic spectroscopy to a high degree of accuracy. Later Dirac showed how the marriage of quantum mechanics and special relativity leads to a prediction of g=2 for fermions. Today the g value of the electron is one of the best-known quantities in physics (measured to 14 decimal places)[2]. The correction of the value of g=2 is fully explained by quantum field theory.
In the present experiment we investigate this internal angular momentum of the electron without the added complication of orbital angular momentum. The spin degree of freedom - in contrast to orbital angular momentum - has nothing to do with the orbiting motion of the electrons. The classical analogy of a spinning particle is also inappropriate, since there is not much meaning to a spinning point particle. As explained above, for the intrinsic spin angular momentum variable the interaction energy with a magnetic field requires a special choice for the gyro-magnetic ratio, namely g=2. For magnetic fields that can be created in the laboratory (sub-Tesla range) the interaction energies given by eq. (4) correspond to radiofrequencies ranging up to microwaves as B is increased (verify this. i.e. calculate frequencies and wavelengths for a few examples). Thus, we need a mechanism to perform the excitation, and a way to measure the relationship between the transition frequency and the magnetic field strength. Electron spin resonance solves both problems in an elegant way, we measure the energy splitting between the two spin levels in the ground state of the spatial motion directly.
To make the experiment work one modulates the external magnetic field with a low-frequency AC signal component (60 cycles). For a fixed radiofrequency one is then able to sweep through a range of B values, such that at a particular phase (time) the resonance condition is met, and this condition will happen periodically. By observing the DC current through the transmitting coil in coincidence with the voltage used to generate the external magnetic field one can find out at what strength of the magnetic field the resonance condition is met. For this technique to work, one has to know that the relaxation times for the electrons are shorter than the time constant of the modulating field. If this is not the case, then less than half of the electrons in the sample would be available for excitation, and the signal might deteriorate too rapidly for detection to occur.
A note about the directions of fields and polarizations used in this experiment; The transition that we are driving in this experiment is a magnetic-dipole transition- meaning that it is the magnetic field component of the radio-frequency radiation which is driving the transition. Also, note that we are transitioning from an ms=-1/2 to ms=+1/2 state. This type of transition (Δms=1) requires a circularly polarized driving field. The axis of quantization in this experiment is defined by the DC magnetic field created by the Helmholtz coils, so we need an RF magnetic field circularly polarized with respect to the DC magnetic field. The RF-coil used generates a linearly-polarized magnetic field along its axis. If the coil were aligned such that the RF-coil was along the axis of the DC-magnetic field from the Helmholtz coil, we would never drive the transition of interest. However, if the RF-coil was perpendicular to the DC magnetic field, then it can be shown that the a linearly-polarized field aligned perpendicularly to an axis of quantization is equivalent to a circularly-polarized field with respect to the axis of quantization. Therefore, in this experiment, the RF-coil is aligned perpendicular to the axis of the DC-magnetic field. (Be sure you understand this concept).
Procedure
To prepare for the experimental setup read through ESR Control Unit, Electron spin resonance at DPPH and Passive RF Oscillator.
Part I: Verify the detection technique for the resonance condition.
A radiofrequency generator is connected to a probe with an inductance (three exchangeable coils with different inductances) L, and a variable capacitor C. Changing the capacitance results in an adjustable frequency range for each coil allowing us to scan between approximately 20 and 100 MHz. A digital frequency meter is built into the control box that contains the radio-oscillator, as well as the power supply for the Helmholtz coils for the magnetic field. Note that the oscillator is split into two parts with the electronics residing in the control box, and the frequency-determining components L and C (and an amplitude control potentiometer) residing in the probe.
A receiver circuit made up of a coil and a variable capacitance is brought close to the radiating coil. It is connected to an AC voltmeter that indicates the strength of the received signal. For fixed transmitter frequency one varies the receiver's capacitor until the receiver circuit matches the transmitter (i.e. achieve resonance). Observe how the receiver shows a strong signal on resonance, how the DC current through the transmitting coil drops on resonance, and how the frequency of the transmitting circuit detunes. Compare this to the resonance problem of classical mechanics (damped driven harmonic oscillator). Detuning is related to the fact that the resonance condition has a slight dependence on the damping constant. Describe your observations in the write-up. This part demonstrates that a transmitter (oscillator) reacts to the conditions of the space surrounding it (mathematically speaking: you are changing the boundary conditions in the Maxwell equations, and creating a load that affects the transmitting coil). The damping effect is not much different from the one obtained by putting an iron core into a coil, thereby forcing the alternating B field to do work on the electron spins in the iron core which would introduce damping in the oscillator circuit.
Part II: Calibrate the magnetic field produced by the Helmholtz coils for a known DC current.
Note that you have to place the two coils accurately at a separation a that corresponds to their radius R. Use the result from Biot-Savart's law for a single coil for the magnetic field strength for a given current along its axis as a function of the separation from the coil d:
| (6) |
To obtain the field generated by two coils separated at distance a=R (many first-year physics texts have this problem, e.g., Fishbane, Gasiorowicz, Thornton 2nd ed. Q 65 on p. 835). Here μ0 is not the same μ as in eq. (1)! Note that the current in Biot-Savart law is the current through each coil and not necessarily the total current in the circuit (You can use the Leybold manual to check whether your numbers are in the right range). Check the homogeneity of the field for a=R. How does your calibration compare to the Biot-Savart result? The number of turns is noted on the coils as n=320. Calibrate the Gaussmeter to zero for zero current. Does the Earth's magnetic field come into play in this experiment?
Part III: Perform the electron spin resonance experiment.
Read through the Electron spin resonance at DPPH (P6.2.6.2) Physics Leaflet provided by Leybold. Connect the control box to the oscilloscope as outlined in the instructions provided by Leybold using the dual-channel set-up while triggering on the channel displaying the driving voltage for the Helmholtz coils. Understand the function of the controls of the DC current through the Helmholtz coils and the AC modulation by observing the voltage applied to the coil displayed on trace 1 (used to trigger the scope). This voltage is not coincident in time with the strength of the magnetic field. To adjust for that, one can shift the phase with a third control. This will be a one-time adjustment once the resonance condition is met. A phase adjustment is necessary since AC current and voltage are out of phase by about 90 degrees for an inductance. The second trace displays a voltage that is proportional to the DC current passing through the transmitting coil. Without a sample the trace should be a straight line.
Set the oscillator to a given frequency, set the DC current to some value (e.g. total current = 1A), pick a midrange value for the modulating magnetic field. Place the DPPH sample inside the transmitting coil. Vary the magnetic field modulation until dips in the trace representing the DC current through the transmitting coil appear. Due to the modulation in the field two resonant points should occur as the magnetic field passes through a maximum in its sinusoidal shape. Use the phase delay control in the control box to adjust the signal such that the resonant points occur symmetrically with respect to the maximum. This adjustment should be performed only once. It would not be necessary if we used a Gauss probe to measure the magnetic field in AC mode (try this out).
Now reduce the magnetic field modulation to a small value (you will need to decrease the DC component to maintain resonance). You can adjust the DC current through the Helmholtz coils so that the resonance occurs at those points in time where the AC component vanishes. Record the DC current through the Helmholtz coils at this point, since the resonance now occurs at the magnetic field strength corresponding to the DC current alone. Observe the frequency change (detuning) as you remove and re-insert the sample, and record it.
Repeat this measurement for about 15 settings of frequency in 5 MHz intervals. This requires a change in coils. Notice the different amount of detuning for the different coils. Perform a linear least squares fit with estimate of uncertainties. Does the fit pass through zero energy splitting (frequency) at zero current? If not, why not? Determine your value of the gyromagnetic ratio for the 'free' electron in DPPH.
References
- ↑ A.C. Melissinos , Experiments in Modern Physics, Academic Press, (2003).
- ↑ D. Hanneke, S. Fogwell & G. Gabrielse, New Measurement of the Electron Magnetic Moment and the Fine Structure Constant Phys. Rev. Lett. 100,120801 (2008)