Difference between revisions of "Main Page/PHYS 4210/Gamma Ray Spectroscopy"
(Created page with "<h1>Gamma Ray Spectroscopy</h1> <p>In this experiment we study the gamma ray spectra of several radioactive elements to learn about the interaction properties of gamma rays with ...") |
|||
| Line 4: | Line 4: | ||
<h1>Introduction</h1> | <h1>Introduction</h1> | ||
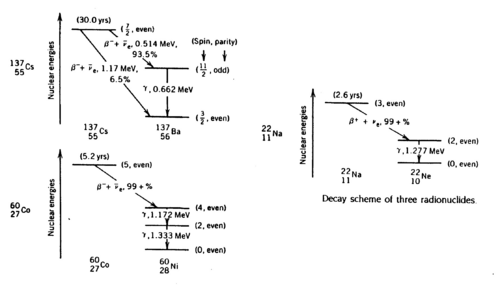
<p>Gamma rays are photons of very short wavelength (~10<sup>-12</sup> cm) or very high frequency (10<sup>22</sup> Hz) that are emitted during nuclear transitions. The decay schemes of the three radionuclides that we study (Na22, Cs137, Co60) are shown below. Read ref. 1-4 to get a clear idea of the significance of the gamma energies.</p> | <p>Gamma rays are photons of very short wavelength (~10<sup>-12</sup> cm) or very high frequency (10<sup>22</sup> Hz) that are emitted during nuclear transitions. The decay schemes of the three radionuclides that we study (Na22, Cs137, Co60) are shown below. Read ref. 1-4 to get a clear idea of the significance of the gamma energies.</p> | ||
| + | <table width=500 align=center><td> | ||
| + | <p align=justify>[[File:Gam-fig1.png|500px|border|center]] | ||
| + | <b>Figure 1 -</b> Decay schemes of Cs-137, Co-60, and Na-22. | ||
| + | <br clear=right> | ||
| + | </p> | ||
| + | </td></table> | ||
| + | |||
| + | <h2>Method</h2> | ||
| + | <p>Photons are electrically neutral, and unlike charged particles, do not experience the Coulomb force. They are, however, carriers of the electromagnetic force, and are able to ionize atoms through their interaction with matter, and this leads to the deposition of energy in the medium as the ionized particle slows down in traversing the medium. This energy can then be detected. The three modes of interaction are: photoelectric effect, Compton scattering, and pair production where the photon interacts with an atom, an electron, and a nucleus respectively. You should read the details of each type of interaction in the references and include this in your write-up. We summarise it briefly below.</p> | ||
| + | |||
| + | <h3>Photoelectric effect</h3> | ||
| + | <p>The photon of energy ''E<sub>g</sub>'' is absorbed by an atom and an electron from one of the shells is emitted. If ''B<sub>e</sub>'' is the binding energy of the electron, then the energy of the emitted electron will have an energy ''E<sub>e</sub>'' = ''E<sub>g</sub>'' - ''B<sub>e</sub>''. Since ''B<sub>e</sub>'' is small (of the order 40 KeV) compared to ''E<sub>g</sub>'' (of the order 1MeV), the electron carries most of the energy of the photon.</p> | ||
| + | |||
| + | <h3>Compton scattering</h3> | ||
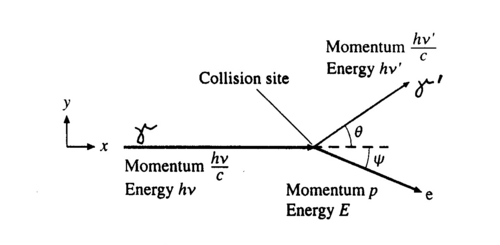
| + | <p>The photon scatters off an electron that is either free or is loosely bound in the atom, thereby scattering the electron. It can be shown (do so in your writeup) that the energy of the scattered electron is related to that of the incident photon, the angle of the scattered photon (theta), and the mass of the electron me through the relationship:</p> | ||
| + | <table width=400 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Zee-eqn1.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(1)</b></td></tr></table> | ||
| + | <table width=500 align=center><td> | ||
| + | <p align=justify>[[File:Gam-fig2.png|500px|border|center]] | ||
| + | <b>Figure 2 -</b> Compton scattering. | ||
| + | <br clear=right> | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <p>Hence the scattered photon (of energy hv’) has the freedom to move at any angle with respect to the incident photon (or gamma ray, as we call it here), whereas the scattered electron is bound by the laws of conservation of momentum to only go in the forward direction. The kinetic energy of the Compton electron is E<sub>C</sub> = hv- hv’. This, combined with the above formula for the energy of the electron shows that the maximum kinetic energy of the electron is when theta = 180° ,i.e., when the photon is scattered backwards. This maximum is known as the Compton edge. </p> | ||
| + | |||
| + | <h3>Pair production</h3> | ||
| + | <p>If the photon has more than twice the rest mass of an electron (0.511 MeV), the photon can produce an electron-positron pair. This must be done in the Coulomb field of the nucleus to balance linear momentum, as the photon cannot produce a pair in free space (its center of mass would have zero momentum). The energy in excess of the rest masses of the products is imparted as kinetic energy. </p> | ||
| + | <p. | ||
Revision as of 12:59, 28 July 2011
Contents
Gamma Ray Spectroscopy
In this experiment we study the gamma ray spectra of several radioactive elements to learn about the interaction properties of gamma rays with matter. The gamma rays are detected through ionization of the material in a scintillation counter, and the output pulse, which is generated with a photomultiplier tube, is then recorded with the aid of a Multi Channel Analyser (MCA) connected to a computer interface. The different types of interaction of gamma rays with matter are understood from a detailed analysis of the observed spectra. Thus, this experiment not only illustrates the physics of the interaction properties of photons, but also introduces scintillation detectors and relevant electronics.
Introduction
Gamma rays are photons of very short wavelength (~10-12 cm) or very high frequency (1022 Hz) that are emitted during nuclear transitions. The decay schemes of the three radionuclides that we study (Na22, Cs137, Co60) are shown below. Read ref. 1-4 to get a clear idea of the significance of the gamma energies.
|
Figure 1 - Decay schemes of Cs-137, Co-60, and Na-22.
|
Method
Photons are electrically neutral, and unlike charged particles, do not experience the Coulomb force. They are, however, carriers of the electromagnetic force, and are able to ionize atoms through their interaction with matter, and this leads to the deposition of energy in the medium as the ionized particle slows down in traversing the medium. This energy can then be detected. The three modes of interaction are: photoelectric effect, Compton scattering, and pair production where the photon interacts with an atom, an electron, and a nucleus respectively. You should read the details of each type of interaction in the references and include this in your write-up. We summarise it briefly below.
Photoelectric effect
The photon of energy Eg is absorbed by an atom and an electron from one of the shells is emitted. If Be is the binding energy of the electron, then the energy of the emitted electron will have an energy Ee = Eg - Be. Since Be is small (of the order 40 KeV) compared to Eg (of the order 1MeV), the electron carries most of the energy of the photon.
Compton scattering
The photon scatters off an electron that is either free or is loosely bound in the atom, thereby scattering the electron. It can be shown (do so in your writeup) that the energy of the scattered electron is related to that of the incident photon, the angle of the scattered photon (theta), and the mass of the electron me through the relationship:
| (1) |
|
Figure 2 - Compton scattering.
|
Hence the scattered photon (of energy hv’) has the freedom to move at any angle with respect to the incident photon (or gamma ray, as we call it here), whereas the scattered electron is bound by the laws of conservation of momentum to only go in the forward direction. The kinetic energy of the Compton electron is EC = hv- hv’. This, combined with the above formula for the energy of the electron shows that the maximum kinetic energy of the electron is when theta = 180° ,i.e., when the photon is scattered backwards. This maximum is known as the Compton edge.
Pair production
If the photon has more than twice the rest mass of an electron (0.511 MeV), the photon can produce an electron-positron pair. This must be done in the Coulomb field of the nucleus to balance linear momentum, as the photon cannot produce a pair in free space (its center of mass would have zero momentum). The energy in excess of the rest masses of the products is imparted as kinetic energy.
<p.