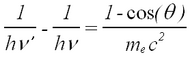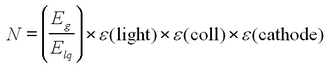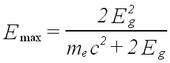Difference between revisions of "Main Page/PHYS 4210/Gamma Ray Spectroscopy"
| Line 140: | Line 140: | ||
<ul> | <ul> | ||
<li>High-Voltage to PMT: 970V (set on the actual power supply)</li> | <li>High-Voltage to PMT: 970V (set on the actual power supply)</li> | ||
| − | <li>Electronic Gain: | + | <li>Electronic Gain: 2</li> |
| − | <li>Digital Gain: | + | <li>Digital Gain: 2048</li> |
<li>Integration Time: 0.625</li> | <li>Integration Time: 0.625</li> | ||
</ul> | </ul> | ||
Revision as of 12:18, 4 October 2013
Contents
Gamma Ray Spectroscopy
In this experiment we study the gamma ray spectra of several radioactive elements to learn about the interaction properties of gamma rays with matter. The gamma rays are detected through ionization of the material in a scintillation counter, and the output pulse, which is generated with a photomultiplier tube, is then recorded with the aid of a Multi Channel Analyser (MCA) connected to a computer interface. The different types of interaction of gamma rays with matter are understood from a detailed analysis of the observed spectra. Thus, this experiment not only illustrates the physics of the interaction properties of photons, but also introduces scintillation detectors and relevant electronics.
Key Concepts
|
|
Introduction
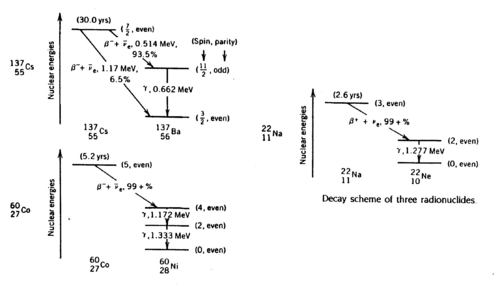
Gamma rays are photons of very short wavelength (~10-12 cm) or very high frequency (1022 Hz) that are emitted during nuclear transitions. The decay schemes of the three radionuclides that we study (Na22, Cs137, Co60) are shown below. Read ref. 1-4 to get a clear idea of the significance of the gamma energies.
|
Figure 1 - Decay schemes of Cs-137, Co-60, and Na-22.
|
Method
Photons are electrically neutral, and unlike charged particles, do not experience the Coulomb force. They are, however, carriers of the electromagnetic force, and are able to ionize atoms through their interaction with matter, and this leads to the deposition of energy in the medium as the ionized particle slows down in traversing the medium. This energy can then be detected. The three modes of interaction are: photoelectric effect, Compton scattering, and pair production where the photon interacts with an atom, an electron, and a nucleus respectively. You should read the details of each type of interaction in the references and include this in your write-up. We summarise it briefly below.
Photoelectric effect
The photon of energy Eg is absorbed by an atom and an electron from one of the shells is emitted. If Be is the binding energy of the electron, then the energy of the emitted electron will have an energy Ee = Eg - Be. Since Be is small (of the order 40 KeV) compared to Eg (of the order 1MeV), the electron carries most of the energy of the photon.
Compton scattering
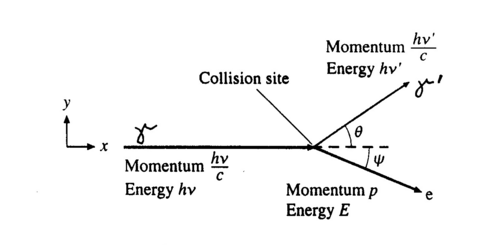
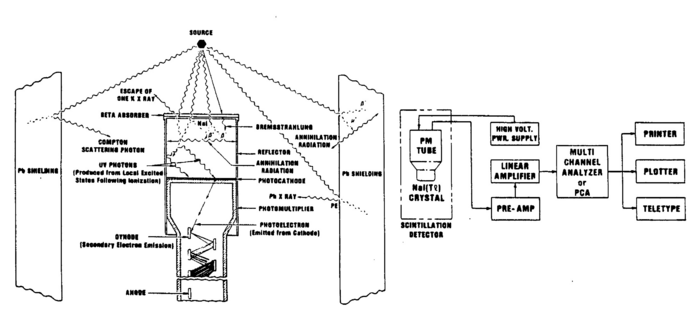
The photon scatters off an electron that is either free or is loosely bound in the atom, thereby scattering the electron. It can be shown (do so in your writeup) that the energy of the scattered electron is related to that of the incident photon, the angle of the scattered photon (theta), and the mass of the electron me through the relationship:
| (1) |
|
Figure 2 - Compton scattering.
|
Hence the scattered photon (of energy hv’) has the freedom to move at any angle with respect to the incident photon (or gamma ray, as we call it here), whereas the scattered electron is bound by the laws of conservation of momentum to only go in the forward direction. The kinetic energy of the Compton electron is EC = hv- hv’. This, combined with the above formula for the energy of the electron shows that the maximum kinetic energy of the electron is when theta = 180° ,i.e., when the photon is scattered backwards. This maximum is known as the Compton edge.
Pair production
If the photon has more than twice the rest mass of an electron (0.511 MeV), the photon can produce an electron-positron pair. This must be done in the Coulomb field of the nucleus to balance linear momentum, as the photon cannot produce a pair in free space (its center of mass would have zero momentum). The energy in excess of the rest masses of the products is imparted as kinetic energy.
The energy dependencies of the three processes are quite different. At energies below a few KeV, the photoelectric effect dominates and the Coulomb effect is small, while pair production is energetically impossible. For the region of 0.1 to about 10 MeV, Compton scattering dominates. Above this, pair production is the predominant method for the interaction of the photons. It is important to realize that in photoelectric effect and pair production, the photon is eliminated in the process of the interaction, whereas in Compton scattering, the energy of the photon is only degraded. As explained further below the various processes involved lead to a complete or incomplete energy deposition of the gamma energy in the scintillator. We have to be concerned only with the first two methods; the photoelectric effect leads to complete energy deposition, while the Compton effect can lead to processes where the scattered gamma ray leaves the detector without depositing its energy.
The Radioactive Sources
You will be working with three radioactive sources: Na22, Cs 137, and Co60. You should note the radiation dosage marked on the source, and read about radiation safety and how to handle radiation sources from ref. 1, pg 326-328. Calculate the number of disintegrations per second for each of the sources based on the quoted dosage.
The Detector
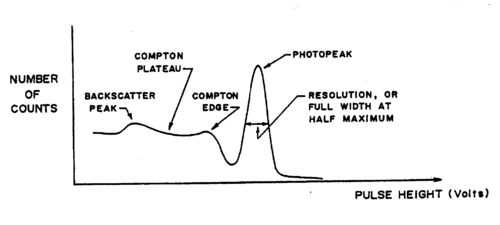
The gamma rays that are emitted from the source are detected with a scintillator detector. In our laboratory, we use inorganic crystals of sodium iodide doped with impurity centres of thallium. This combination is denoted by NaI(Tl). A photon entering the detector ionizes the material through the processes described above. The positive ions and electrons created by the incoming photon diffuse through the lattice and are captured by the impurity centres i.e. the Tl atoms, which act as luminescence centres. Recombination produces an excited centre,which emits visible light upon its return to the ground state. The efficiency of these inorganic crystals is high, but the light output is spread over a time interval of the order of microseconds.
In general, for gamma rays less than 1 MeV, photons undergoing the photoelectric process will be completely absorbed and will give rise to a determined number of light quanta. These light quanta are then seen by the photomultiplier tube, and the output pulse will be proportional to the incoming energy of the gamma ray. The energy of the electrons produced by the Compton effect will depend on the angle at which they are scattered and hence there will be a spectrum of detected pulses. At energies above 1 MeV, pair production can occur and the electron and positron lose their kinetic energy by ionizing the medium. The electron is absorbed, while the positron annihilates within a few nanoseconds into two photons, each of 0.511 MeV. These may then interact through the photoelectric or Compton effect. There are three possibilities for the observed energy (show this in the writeup) depending on whether none, one or both of these photons from the positron annihilation are detected.
As mentioned, the produced light is proportional to the energy of the incident gamma ray. This light is then made incident on the photocathode face of a photomultiplier tube (PMT), which converts the photons to photoelectrons through the photoelectric effect. The electrons are amplified and then converted to a voltage pulse. The PMT used here has 10 stages and the multiplication for such tubes is about 106 for an operational voltage between the cathode and the anode of 1000V. The cascade of electrons produced at each of the multiplication stages of the dynodes is collected at the anode, converted to a voltage pulse, which is then amplified and analysed. The PMT is enclosed in a high permeability material to shield against magnetic fields, as such effects would affect the efficiency of the tube.
Note that the metal shield that encloses the scintillator crystal does not allow β (or other charged) particles to permeate and deposit their usually well-defined energies. Thus, you should not expect to observe structures associated with, e.g., the 0.514 MeV and 1.17 MeV electrons coming from the Cs137 source with branching ratios of 93.5% and 6.5% respectively (cf.. Fig. 1). Charged particles are created inside the crystal by γ ray impact. There will be, however, backscattered γ rays from Compton scattering outside the crystal, e.g., off the backing of the source and off the lead shield.
Read the specifications for the model of the scintillator detector and photomultiplier that you have. Note that the size of the crystal is small. How does this affect your results? The typical quantum efficiency of scintillators of this type is one photon of light produced per 100 eV of energy deposited in the scintillator. The width of the full-energy peak (i.e. when the gamma energy is fully absorbed) depends on the number of light quanta produced by the incident gamma ray. The energy resolution, dE/E is an important quantity to consider as this factor will determine if we can separate gamma rays very close in energy.
The chain of events may help illustrate this point. The incident gamma ray of energy Eg produces a photoelectron with energy Ee ~ Eg. The photoelectron produces N light quanta in the scintillator material via ionization and excitation, each with an energy Elq. Since the light is visible (~400 nm), Elq is about 3 eV. This light falls on the photocathode, which has a quantum efficiency or sensitivity to the wavelength of the incident light. For the tube supplied, the efficiency peaks near 400 nm, making it quite suitable for use with a scintillator. Let
- ε(light) be the efficiency for the conversion of the excitation energy into light quanta
- ε(coll) be the efficiency for collecting the n lq light quanta at the photocathode of the PMT
- ε(cathode) be the efficiency for the cathode to eject a photoelectron
Then, the number of photoelectrons produced at the photocathode is
Typical values for the efficiencies for NaI detectors are:
- ε(light) = 0.1
- ε(coll) = 0.4
- ε(cathode) = 0.2
For a 1MeV gamma ray, this yields about 3x103 photoelectrons at the photocathode. All the processes mentioned above are subject to statistical fluctuations, and contribute to the broadening of the line width. In addition, there is a contribution from the statistical process due to the multiplication of the photoelectrons in the stages of the PMT.
The Multichannel Analyser
The electrons collected at the anode of the PMT pass directly into the Bridgeport eMorpho MCA. This pulse of electrons is passed across a resistor whose value is set by the user (using the "electronic gain" parameter). The voltage across this resistor is digitized into one of 4096 bins according to its maximum value (peak height)- this process of converting an analog voltage into a digital value is called analog-to-digital conversion (ADC). The MCA performs this task for all pulses and creates a histogram of counts in each ADC bin.
There are several important parameters which affect the performance of the MCA.
- Electronic Gain: As mentioned above, setting this parameter changes the value of the resistance that the PMT current is being passed through. The allowed values are 0-100 Ohm, 1-430 Ohm, 2- 1100 Ohm, 4- 3400 Ohm.
- Digital Gain: Once passing through the ADC, the resulting value can then be further scaled by this amount. This is useful if one is trying to match up bin number to a calibrated energy in eV.
- Trigger Threshhold : The amount above the average background which is required for the MCA to accept a particular pulse and record its statistics in the histogram.
- Run Time: The length of time for which to acquire data.
- Integration Time: Each combination of scintillator/PMT will have a characteristic decay time for the pulses. This parameter sets the time for which the MCA averages the data, and should be set to roughly the 1/e time of the pulse decay.
- High Voltage: The parameter "high voltage" in the MCA client software does nothing. Bridgeport makes an HV supply for PMTs which connect directly to the eMorpho. We are using a separate power supply, hence adjusting this parameter in the software does nothing. However, changing the 1000V supplied to the PMT from the power supply will mean that more electrons are collected per pulse. If this dc voltage is set too high and and too many photons are present, there could be a buildup of charge inside the PMT and catastrophic damage could occur.Please do not change the setting of the voltage to the PMT from 1000V.
- Hold off time: This is the time after detection of a pulse for which the MCA will not register the detection of another pulse. In practice, this should be set to a few times the 1/e decay time of a pulse to avoid another trigger event occurring from the decay of the pulse which was just recorded.
There are two programs required for the computer to be able to get data from the eMorpho MCA. First, MDS.exe on the desktop needs to be run in order to start the data server. Second, the software to control the settings and acquire data is EMorpho Client v1.0.exe and is on the desktop. Run this program and become familiar with its control for monitoring in the pulse height and taking a histogram.
The signal from the PMT is directly input to a multichannel analyser which is a device that sorts incoming pulses according to pulse height and keeps count of the number at each height in a multichannel memory. The contents of each channel is displayed on a screen to give a pulse height spectrum, which is then analysed. The amplitude of the incoming pulse is digitized with an Analogue to Digital Converter (ADC), and sorting is done based on how many pulses had a particular value of the digitized amplitude. The total number of channels into which the voltage range is digitized determines the resolution of the MCA. Read the Bridgeport eMorpho manual to understand the characteristics of the electronics you are supplied with, and to learn more about the ADC range and resolution that can be achieved. Read ref. 1, 2, 4 to understand the functions of a MCA. Review what is meant by ‘dead time’ and ‘live time’. Do not operate with a dead time of more than 30%, since too high count rates can cause the electronics to misbehave.
To understand this experiment it is crucial to observe the pulses fed from the scintillator/PMT to the MCA. This can be done using the Bridgeport eMorpho Client v1.0 on the desktop. This is the software which controls the parameters of the MCA and displays the acquired data. By selecting the "Pusle" icon along the top, you can observe the shape of pulses coming from the MCA. You will observe high-amplitude pulses (high energy was recorded since many visible photons were produced), as well as lower-amplitude pulses occurring randomly in rapid succession. The MCA records the pulse heights and the software assembles them into a histogram according to channel number. One can then calibrate the channels using known gamma sources.
The natural linewidth of the gamma rays is extremely narrow (a few eV compared to the MeV range of the energies themselves!). The broadening observed in the recorded spectra is a result of the detection method (a cooled Germanium detector would show these lines being much narrower, but again at a resolution that depends on the detector itself). It is important to realize on the example of the Cs137 spectrum, for which a single energy at 0.662 MeV is expected that several effects occur in ‘real life’:
- Broadening of the photopeak at 0.662 MeV.
- A Compton background (plateau) with two edges: at the higher end, below the
photopeak a maximum electron(!) energy of
Understand this result using eq. (1). At lower energies in the Compton plateau a distinct photopeak corresponding to backscattered gamma rays whose energy follows from eq. (1) for θ = π. Note how nearly backscattered gammas give about the same energy due to the slow variation of the cos function for θ = π.(2) - A fluorescent K-shell Xray peak caused by soft gamma rays hitting the shielding material (typically lead), knocking out K-shell electrons. The vacancies are typically filled from the L-III shell (2p±1). Use the CRC Handbook (see Lab Technologist or Library) to verify that the difference in energy results in characteristic X rays of about 75 keV for Pb.
A typical spectrum is shown in Fig. 2 on a linear scale. If we go to a logarithmic scale (the MCA software allows to do this), we find an additional weak peak at about twice the gamma energy. This is the so-called sum peak, which arises when two gamma rays from uncorrelated decay events are depositing their energy in the scintillator within a fraction of a microsecond, i.e., the timescale over which the scintillation in the crystal and photomultiplication in the tube occurs. You should be able to observe sum peaks in this experiment when accumulating enough statistics. The peaks appear more strongly when the source is brought closer to the PMT.
|
Figure 3 - Typical Cs-137 spectrum using an NaI(T1) scintillator.
|
Besides sum peaks another complication can occur for high-energy gamma rays. When pair creation is an important energy deposition mechanism, so-called escape peaks are observed. These correspond to events where one or more of the created electrons/positrons escape the crystal without giving up their energy. Such peaks occur at Eg - j (0.511 MeV), where j is the number of escaped electrons/positrons. Since we do not use sources with Eg > 2 MeV in this experiment, we do not find this complication in our spectra.
Experimental Procedure
While conducting the experiment, make sure that only the source whose spectrum you are observing is near the apparatus otherwise your calibration results will be skewed. Take only one source out at a time, and keep the others in the lead shielding box. Be careful while handling sources. Become familiar with the documentation and all the apparatus before starting. However, be innovative and see how different settings of e.g. the ADC or the amplifier change your results.
Settings
Please ensure the following running parameters
- High-Voltage to PMT: 970V (set on the actual power supply)
- Electronic Gain: 2
- Digital Gain: 2048
- Integration Time: 0.625
Ensure the following connections: the scintillator and PMT is connected, the HV output from the power uspply is connected to the PMT, the signal output from the PMT is connected to the MCA, and the MCA is connected to the computer.
In our setup, we have mounted the PMT vertically, allowing you to place the source on a tray at several different distances from the source. Once you have found an optimal distance for all three sources (i.e. you do not get ‘pile up’ effects (see Leo)), it is best to use this distance for calibration and determination of the peak energies. However, in the last part of the experiment you will be asked to draw qualitative conclusions by placing a source at varying distances.
|
Figure 4 - Gamma source, NaI(T1) detector, PMT, lead shield showing relevant processes.
|
Follow the instructions outlined in Experiment 2.1 for gamma ray calibration from Duggan in the red binder in the lab. In brief, place the Cs137 source 1.5 inches (5 cm) away from the face of the detector. Turn on the HV supply.
Question: Explain how a single channel and a multi channel analyzer work.
The Cs source emits a gamma ray of 662 KeV (note that the energies must be in keV for the auto calibration to work!). Locate the peak for the ‘full containment’ gamma ray and find the maximum, which will give the channel number. Enter the channel number and the corresponding energy value (662) in the Energy Scale entry for energy calibration.
Print the spectrum after accumulating data for enough time such that the statistical errors are small. Explain all the peaks on this curve. Note the channel number at which the peak energy occurs. Note that the calibration is valid only for the chosen amplifier gain, that the zero channel does not necessarily correspond to zero energy, and that a ‘flooding’ of low-energy channels can be avoided by setting a threshold in the MCA software!
Remove the Cs137 source, place it back in the lead container and insert the Co60 source into the holder at the same distance from the detector. Record the positions of the two gamma peaks at 1173 KeV and 1332 keV as above, and enter the channel values and energies in the energy calibration. Now you have calibrated the device using the three energies and three channel values.
Print the spectrum of the Co60 source. Explain all the peaks on your spectrum. Do you get the ‘sum peak’? (Set the display to a logarithmic scale). If not, adjust the collimator until you do. Explain why this peak occurs. Does it occur at the value you expect? Put a sheet of lead on the shelf and then place the source. How does the spectrum change? Now place a sheet of lead on top of the source. What, if anything, has changed in the spectrum? You may have to move the source closer or farther from the detector to observe the backscattering signals.
Remove the Co60 source, place it back into the lead container, and place the Na22 source on the holder. The Na22 has a gamma ray energy at 1277 KeV. What value of the maximum position do you find based on your calibration curve? Is this consistent with the resolution dE/E? Note, this source is relatively weak, so you will have to take data from many minutes. What is its present activity (note the date mark on the source)?
You will notice that the predominant peak is not this one, but one at a lower energy. What energy does this peak occur? What is this peak due to, and what energy value do you expect this peak to occur?
Print the spectrum and explain all the interesting details. Create a calibration curve for all three sources i.e. a plot of the energy of the peak and the centroid of the peak. What is the error of a straight line fit to this curve? If the fit is poor, you have made a mistake in assigning peak-channel values, and may have to repeat the analysis. Discuss sources of error.
- Obtain the energy resolution for the photopeak for Cs137 and for one of the Co60 peaks. Does this agree with what you have learned about scintillator devices?
- Place the Cs137 source at varying distances from the detector and explain qualitatively the rates that you observe. Put the source at slot 2 below the detector, and place first one, then two, and then three sheets of lead on top of the source. Comment on the rates, and the reason for the observed behaviour. Repeat for sheets of aluminum.
- Attain an unknown source from the Lab Technologist. Use your now-calibrated gamma-ray spectrometer to identify the radio isotope(s) in the unknown source.
References
- Preston and Dietz, The Art of Experimental Physics, Wiley.
- J.L. Duggan, Laboratory Investigations in Nuclear Science, Tennelec.
- A.C. Melissinos, Experiments in Modern Physics, Academic Press.
- Leo, Techniques for Nuclear and Particle Physics Experiments, Springer-Verlag.
- H. Frauenfelder and Henley, Subatomic Physics.
- K. Siegbahn, Alpha, Beta, and Gamma-Ray Spectroscopy, vol. I, chpts 5,8a.