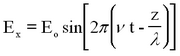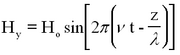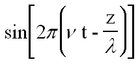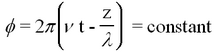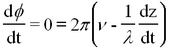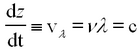Difference between revisions of "Main Page/PHYS 3220/Speed of Light"
| Line 35: | Line 35: | ||
<p>Referring to Fig. 1, the distance travelled by the light pulse is</p> | <p>Referring to Fig. 1, the distance travelled by the light pulse is</p> | ||
| − | <table width= | + | <table width=600 align=center><tr><td> |
| − | <p align=justify>[[File:C-eqn4.png| | + | <p align=justify>[[File:C-eqn4.png|400px|center]] |
</p> | </p> | ||
</td><td><b>(1)</b></td></tr></table> | </td><td><b>(1)</b></td></tr></table> | ||
Revision as of 08:14, 19 July 2011
Introduction
Light can be described as a periodic electromagnetic plane wave which carries energy in the form of an electromagnetic field. The electric and magnetic components can be written as:
This represents a monochromatic (single-frequency) beam travelling in the + z direction having a wavelength λ and frequency v (related by λ ν = c). The angle
is called the phase of the plane wave. A point on the wave having a constant phase (e.g. the peak of a sine wave) moves at a velocity determined by setting the time derivative of the constant phase equal to zero
The latter quantity vλ is called the phase velocity of the plane wave. From the above we find that in vacuum the phase velocity of monochromatic light is frequency (colour) independent. This quantity is known to high precision and is called the velocity of light c. We will determine the value of c in this experiment.
This experiment uses pulses of light reflected from a spinning mirror, and thus a band of frequencies is present centered around the fundamental optical frequency. An accurate analysis requires the concept of a group velocity. Due to the length of the pulses we may treat the light as monochromatic in our experiment, and thus do not need to distinguish between group and phase velocities.
Method
Many methods for the determination of the speed of light have been developed. Since c = Δs / Δt is large, i.e. ~3 x 108 m/sec., its measurement in the laboratory necessitates the measurements of small time increments Δt, for modest values of Δs. One may employ large path lengths of celestial dimensions to increase Δt to a value which may be recorded more accurately. This latter method was used in 1675 by Roemer (Δs = 1.86 x 108 miles (the diameter of the Earth's orbit) gives Δt = 1000 sec). One can also perform the timing of the passage of light from its source to a distant mirror and then back to the source.
The rotating mirror method of Foucault, and later Michelson, provides a compromise between these two approaches. In this experiment (Fig. 1), a beam of light from a laser is reflected from a rotating mirror (M1) along a measured path by way of a series of secondary mirrors (M2, M3, M4, M5), which reflect it back along the original path to the rotating mirror. While the light pulse has been travelling along this path, the mirror has rotated slightly so that the returning light pulse reflected from the new position of the mirror will be deviated a small distance Δx from its original path. Relating the resulting deflection of the returning beam to the time taken for the mirror to rotate, and thus to the known path length, c is determined.
Referring to Fig. 1, the distance travelled by the light pulse is
| (1) |