Difference between revisions of "Main Page/PHYS 3220/Thermionic"
| Line 21: | Line 21: | ||
<p>From Fig. 2, note two distinct regimes of operation: a region (known as the space-charge limited region) where I<sub>a</sub> increases rapidly with V<sub>a</sub>; and the saturation region (known as the temperature limited region). At low anode voltages the cathode is surrounded by a dense space-charge of electrons, which are being continually emitted and reabsorbed. Only those electrons which are well away from the cathode are drawn towards the anode, since the electrostatic potential of the electron cloud counteracts the accelerating potential. A separate discussion of the current-voltage characteristic for this region follows below (eq. 2). As the anode voltage is increased, more electrons are drawn out of the space charge region toward the anode. For sufficiently high voltages the space-charge disappears and the beam current is limited by the rate of emission from the cathode, which leads to a saturation of the current. This saturation current depends on the temperature of the emitter and its work function, and is given by the Richardson-Dushman equation (cf.. ref. 1), </p> | <p>From Fig. 2, note two distinct regimes of operation: a region (known as the space-charge limited region) where I<sub>a</sub> increases rapidly with V<sub>a</sub>; and the saturation region (known as the temperature limited region). At low anode voltages the cathode is surrounded by a dense space-charge of electrons, which are being continually emitted and reabsorbed. Only those electrons which are well away from the cathode are drawn towards the anode, since the electrostatic potential of the electron cloud counteracts the accelerating potential. A separate discussion of the current-voltage characteristic for this region follows below (eq. 2). As the anode voltage is increased, more electrons are drawn out of the space charge region toward the anode. For sufficiently high voltages the space-charge disappears and the beam current is limited by the rate of emission from the cathode, which leads to a saturation of the current. This saturation current depends on the temperature of the emitter and its work function, and is given by the Richardson-Dushman equation (cf.. ref. 1), </p> | ||
| + | |||
| + | |||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Th-eqn1.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(1)</b></td></tr></table> | ||
| + | |||
| + | <p>where : | ||
| + | <ul> | ||
| + | <li>Jo = saturation current density</li> | ||
| + | <li>A = a proportionality constant given below</li> | ||
| + | <li>T = temperature of the emitter in K</li> | ||
| + | <li>W = work function of the metal of the emitter</li> | ||
| + | <li>k = Boltzmann constant</li> | ||
| + | </ul> | ||
| + | </p> | ||
| + | |||
| + | <table width=200 align=center> | ||
| + | <td> | ||
| + | <p align=justify>[[File:Th-eqn1b.png|160px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
Revision as of 08:56, 21 July 2011
Thermionic Emission
It is well known that when a metal is heated to high temperatures it emits electrons, as in the case of the filament in an electron tube. This phenomenon of thermionic emission is called the Richardson Effect, and was discovered by Thomas Edison in 1883. It is explained by the electron theory of metals and is comparable to the evaporation of liquids. To obtain a thermionic current, both the emitter and the collector are placed in an evacuated vessel and an electric field is applied.
Theory
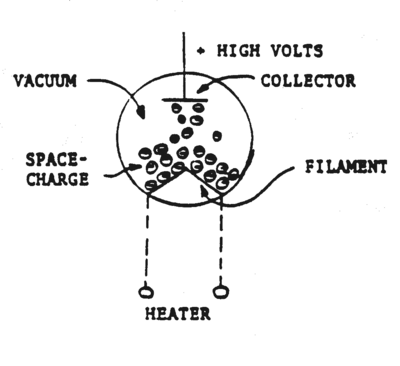
Consider a vacuum diode as shown in Fig. 1. The filament (usually a tungsten wire) is heated to a temperature in the vicinity of 2500o K. The electrons emitted by the filament (cathode) are drawn to the collector (anode) when the anode is raised to a high potential (0 to 400 Volts).
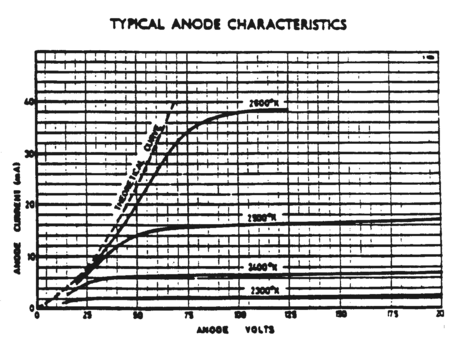
Typical current voltage characteristics Ia vs. Va for various values of filament temperature are shown in Fig. 2.
|
Figure 1 |
Figure 2
|
From Fig. 2, note two distinct regimes of operation: a region (known as the space-charge limited region) where Ia increases rapidly with Va; and the saturation region (known as the temperature limited region). At low anode voltages the cathode is surrounded by a dense space-charge of electrons, which are being continually emitted and reabsorbed. Only those electrons which are well away from the cathode are drawn towards the anode, since the electrostatic potential of the electron cloud counteracts the accelerating potential. A separate discussion of the current-voltage characteristic for this region follows below (eq. 2). As the anode voltage is increased, more electrons are drawn out of the space charge region toward the anode. For sufficiently high voltages the space-charge disappears and the beam current is limited by the rate of emission from the cathode, which leads to a saturation of the current. This saturation current depends on the temperature of the emitter and its work function, and is given by the Richardson-Dushman equation (cf.. ref. 1),
| (1) |
where :
- Jo = saturation current density
- A = a proportionality constant given below
- T = temperature of the emitter in K
- W = work function of the metal of the emitter
- k = Boltzmann constant