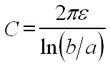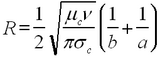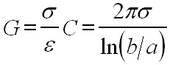Difference between revisions of "Main Page/PHYS 4210/Coaxial Cable"
| Line 11: | Line 11: | ||
<table width=200 align=center> | <table width=200 align=center> | ||
<tr><td> | <tr><td> | ||
| − | <p align=justify>[[File:Coax-eqn1.png| | + | <p align=justify>[[File:Coax-eqn1.png|90px|center]] |
</p> | </p> | ||
</td><td> <b>(1)</b></td></tr></table> | </td><td> <b>(1)</b></td></tr></table> | ||
| Line 22: | Line 22: | ||
</td><td> <b>(2)</b></td></tr></table> | </td><td> <b>(2)</b></td></tr></table> | ||
<p>where ε is the dielectric permittivity of the dielectric layer. </p> | <p>where ε is the dielectric permittivity of the dielectric layer. </p> | ||
| − | |||
<p>Since both inner and outer conductors are not ideal, the line has a resistance per unit length</p> | <p>Since both inner and outer conductors are not ideal, the line has a resistance per unit length</p> | ||
<table width=200 align=center> | <table width=200 align=center> | ||
<tr><td> | <tr><td> | ||
| − | <p align=justify>[[File:Coax-eqn3.png| | + | <p align=justify>[[File:Coax-eqn3.png|160px|center]] |
</p> | </p> | ||
</td><td> <b>(3)</b></td></tr></table> | </td><td> <b>(3)</b></td></tr></table> | ||
<p>Here, μ<sub>c</sub> and σ<sub>c</sub> are the magnetic permeability and conductivity of the conductors, respectively. The resistance value (3) is determined by the skin depth that measures the characteristic distance of penetration of the electromagnetic wave into the conductors. It is within the skin layer that the absorption of the electromagnetic power is most intense. The skin depth, in turn, depends on the frequency, ν, of the wave, hence R depends on ν as well.</p> | <p>Here, μ<sub>c</sub> and σ<sub>c</sub> are the magnetic permeability and conductivity of the conductors, respectively. The resistance value (3) is determined by the skin depth that measures the characteristic distance of penetration of the electromagnetic wave into the conductors. It is within the skin layer that the absorption of the electromagnetic power is most intense. The skin depth, in turn, depends on the frequency, ν, of the wave, hence R depends on ν as well.</p> | ||
| − | |||
<p>Finally, the dielectric separating the two conductors is not ideal, hence there always is a leakage current when the conductors are kept at different potentials. This effect is accounted for by introducing the conductance per unit length of the line</p> | <p>Finally, the dielectric separating the two conductors is not ideal, hence there always is a leakage current when the conductors are kept at different potentials. This effect is accounted for by introducing the conductance per unit length of the line</p> | ||
<table width=200 align=center> | <table width=200 align=center> | ||
<tr><td> | <tr><td> | ||
| − | <p align=justify>[[File:Coax-eqn4.png| | + | <p align=justify>[[File:Coax-eqn4.png|170px|center]] |
</p> | </p> | ||
</td><td> <b>(4)</b></td></tr></table> | </td><td> <b>(4)</b></td></tr></table> | ||
<p>σ being the conductivity of the dielectric layer.</p> | <p>σ being the conductivity of the dielectric layer.</p> | ||
| + | |||
| + | <p><b>Exercise</b>Derive (1) and (2). Hint: to derive (1), suppose that some current ''J'' flows through the inner conductor of the line. Find the value of the magnetic field produced by this current, and then the magnetic field energy stored in a unit length element of the line. This energy also equals ''LJ<sup>2''</sup>/2, from the definition of inductance per unit length. To derive (2), assume that the inner and outer conductors have charges per unit length equal to +''q'' and –''q''. Find the potential difference between the two conductors. From the definition of a unit length capacitance, the potential difference equals to ''qC''.</p> | ||
Revision as of 12:47, 27 July 2011
Coaxial Cable
You should carefully read Experiment 1 in The Art of Experimental Physics, Preston and Dietz. This write-up is meant to supplement that material.
Theory
A coaxial cable (coax) is one of the most popular means for transmitting the electromagnetic power from a generator to a receiver. It consists of an inner and outer conducting lines (usually made of copper) separated by a dielectric layer (usually teflon). The electromagnetic wave can propagate in a coax in the form of TE, TM, and TEM modes, and the latter is the one that is most commonly used. In this experiment, the effect of a coaxial cable on the propagating signal and some physical characteristics of a coax are studied.
There are two levels of description of electromagnetic phenomena. The more fundamental one relies on Maxwell’s equations combined with material equations. Within this approach, one uses the language of electric and magnetic field strengths, potentials, dielectric susceptibility and magnetic permeability, etc. Engineers, however, prefer a simpler language of currents, voltages and lump elements, that is, resistance, capacitance, conductance, and inductance. In order for this simplified description to be applicable to the problem considered, the characteristic sizes of lump elements must be much smaller than the wavelength of an electromagnetic wave. Nevertheless, with a small modification, the approach of engineers allows us to obtain some meaningful results even when this requirement is not met. We will adopt the language of engineers in the following discussion.
The idea of the modification is that, instead of using the net inductance, capacitance, resistance and conductance, we use their values per unit length. Thus, a coax is viewed as a system with distributed parameters. Let us write down the expressions for the unit-length characteristics of a coax. A current in the central conductor sets up a magnetic field; hence, the line has inductance whose value per unit length is
| (1) |
where μ is magnetic permeability of the dielectric layer between the two conductors, and a and b are the radii of the inner and outer conductors, respectively.
Next, the capacitance per unit length between the two conductors is:
| (2) |
where ε is the dielectric permittivity of the dielectric layer.
Since both inner and outer conductors are not ideal, the line has a resistance per unit length
| (3) |
Here, μc and σc are the magnetic permeability and conductivity of the conductors, respectively. The resistance value (3) is determined by the skin depth that measures the characteristic distance of penetration of the electromagnetic wave into the conductors. It is within the skin layer that the absorption of the electromagnetic power is most intense. The skin depth, in turn, depends on the frequency, ν, of the wave, hence R depends on ν as well.
Finally, the dielectric separating the two conductors is not ideal, hence there always is a leakage current when the conductors are kept at different potentials. This effect is accounted for by introducing the conductance per unit length of the line
| (4) |
σ being the conductivity of the dielectric layer.
ExerciseDerive (1) and (2). Hint: to derive (1), suppose that some current J flows through the inner conductor of the line. Find the value of the magnetic field produced by this current, and then the magnetic field energy stored in a unit length element of the line. This energy also equals LJ2/2, from the definition of inductance per unit length. To derive (2), assume that the inner and outer conductors have charges per unit length equal to +q and –q. Find the potential difference between the two conductors. From the definition of a unit length capacitance, the potential difference equals to qC.