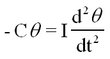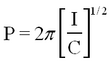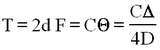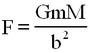Main Page/PHYS 3220/Cavendish

Introduction

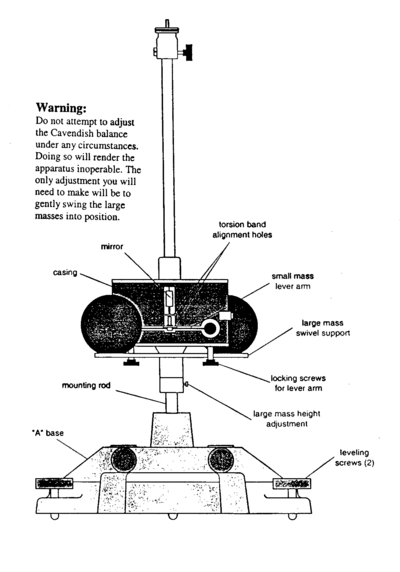
Cavendish first performed the measurement of G, one of the classic experiments in physics, in 1798. The apparatus at your disposal is a modified form of that used by Cavendish and others. The high sensitivity of the apparatus demands patience, perseverance and care from the experimenter. This is a very delicate instrument so treat it gently.

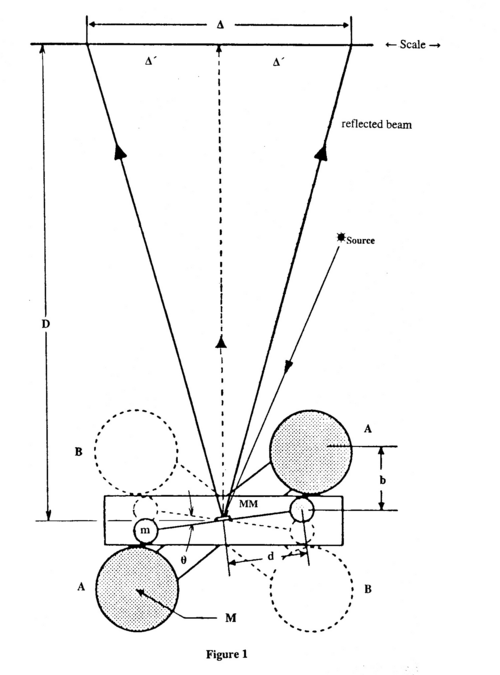
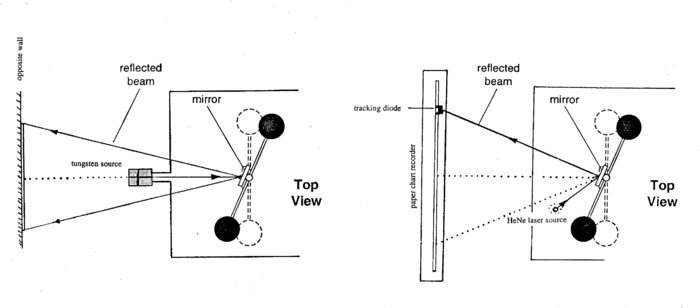
A lamp S (see Fig. 1) illuminates a small (effectively) massless mirror MM that is attached to a light horizontal rod holding two small lead balls of mass m at a separation of 10cm. The small balls and mirror are suspended from a 25cm. bronze torsion wire (perpendicular to the page). The entire apparatus is enclosed in a rigid case that is mounted securely on a wall or table.

When two massive lead balls (each with mass M = 1.5kg) are placed asymmetrically as illustrated, in position AA, a small torque acts on the torsion balance twisting the torsion wire and causing the image of the light source to swing through a measurable distance Δ' along the opposite wall. The swing gradually decays until equilibrium is reached. The massive balls are next placed at diametrically opposite points, BB, for further measurement. After the oscillations have died away once more, a second equilibrium position is reached at a distance Δ' with respect to the other side of the zero position. We will use this pattern to evaluate a value for G, the gravitational constant.

Figure 1 - Experiment setup (Top View).

Method

IMPORTANT: Treat the equipment gently. For example, slamming the door or bumping into the table will considerably lengthen the experimental observation time.

In order for the balance to operate correctly, the torsion wire must be precisely vertical and must be able to move freely. The centres of the four balls must lie in one plane as well.

Both a manual recording technique and the chart recorder method are used in this experiment. The position of the light beam on the scale on the opposite wall is noted when the heavy balls are an equal distance from the small balls. The large balls are then rotated so that they almost touch the case. You should make this adjustment carefully to ensure that the heavy balls do not knock the case. If the case is accidentally knocked, the mirror will be set into a large amplitude oscillation that will take about 1 hour to decay. You can therefore save yourself a lot of time (and effort) by making this adjustment delicately in the first place.

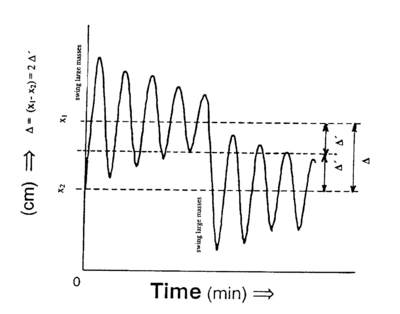
If this step has been completed successfully the position of the light spot on the opposite wall will change slowly with time. Note this position on the scale (a cross wire) every 15 seconds for the first few minutes and every 30 sec. or 1 min. thereafter. The light spot will undergo damped oscillations about an equilibrium position Δ'. Determine the mean period of oscillation P with a stop watch and compare this with the value derived from a plot of displacement vs. time. Allow about 45 min – 60 minfor these oscillations to damp out and measure the new equilibrium position x1 (see Fig. 2).

Figure 2 - Graph of small-mass oscillations.

Carefully reverse the position of the heavy balls and repeat the procedure recording position vs. time and the new position at equilibrium x2. Now repeat this twice more and obtain an average value for Δ. Measure the diameter of the heavy ball and the thickness of the case. Find the separation of the centres of gravity of the two balls. What approximation(s) does this involve? Repeat this experiment with the chart recorder.

Theory

The torque generated by a force F acting on a mass m located at r is defined through the cross product T = r x F. For rotational motion in a plane described by an angle θ(t), angular velocity ω(t), and acceleration α(t) the torque has only a single non-zero component. It is perpendicular to the plane and is denoted by a scalar: T = Tz. The combination of the definition of torque with Newton's law of motion, and the moment of inertia I results in the equation of motion T = I α, where T represents the sum of all torques acting on the system (in our case two small mass’ rotating about their center of mass). The external torque in our case is provided by the angular form of Hooke's law as applicable for the torsion of wires, and we ignore for the moment the internal friction in the wire (which however is crucial to obtain a steady-state solution after long intervals).

If a torsion balance is twisted by a torque (couple) through a small angle θ (radians), the restoring torque is proportional to the angular displacement and is oppositely directed,

i.e., Where C is the torque constant (cf.. spring constant) of the wire. (What are the units of C?) We combine this with the equation of motion to obtain

(1)

Equation (1) is a homogeneous linear ordinary differential equation with constant coefficients. The friction responsible for the damping of the oscillations has been omitted here. Solve the equation and show that the period P is given by

(2)

Neglecting the material between the two small spheres, the moment of inertia I of the torsion balance about the axis of rotation is

(3)

where m = mass of each ball and 2d is the distance between them.

Thus by measuring the period P and calculating I, the torque constant C may be found from equation (2). If Δ' is the deflection of the light beam from the rest position upon rotation of the torsion wire through θ radians, (Fig. 1) then

where D is the distance between the mirror and the scale.

Once the large spheres are moved to their alternate asymmetrical position, the total deflection Δ produced (after the oscillations have died out) is (see Fig. 2)

(4)

The torque (couple) exerted by the large masses is

(5)

Here F is the magnitude of the gravitational force of attraction between the small and large masses, and is given by

where b is the distance between the centres of the small (m) and large (M) masses at equilibrium.

Procedure

Figure 3a - Manual setup. Figure 3b - Tracking setup.

1. Derive G from the above equations in terms of the period of oscillation.
2. Perform your measurements using the two set-ups (manual and automatic recording).
3. Discuss the effect of the attraction of the distant 1.5 kg. sphere for the small balls.
4. Enumerate and discuss other possible sources of error in the measurement of G using this apparatus.
5. When the beam of light oscillates about its final position, it slowly damps out. Assume that the damping force is proportional to the (angular) velocity to find the equation of the motion. From the data, find the damping constant. See textbook references on damped harmonic motion e.g. French's book.
6. Find the expression for the damping force at any time and compare the frequency of the motion without damping to that with damping. Comment on the difference(s) between the two.
7. Why do you need to measure the period of oscillation?

Figure 4 - Cavendish Beam.

References

1. J.E. Beams, Physics Today, May 1971, pp. 32-40.
2. For a discussion on damping see: A.P. French, Vibration and Waves, Norton, pp.62-70.