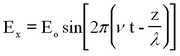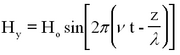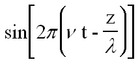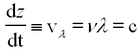Difference between revisions of "Main Page/PHYS 3220/Speed of Light"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
</td></table> | </td></table> | ||
<p>is called the phase of the plane wave. A point on the wave having a constant phase (e.g. the peak of a sine wave) moves at a velocity determined by setting the time derivative of the constant phase equal to zero</p> | <p>is called the phase of the plane wave. A point on the wave having a constant phase (e.g. the peak of a sine wave) moves at a velocity determined by setting the time derivative of the constant phase equal to zero</p> | ||
| + | <table width=400 align=center><td> | ||
| + | <p align=justify>[[File:C-eqn3a.png|140px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <table width=400 align=center><td> | ||
| + | <p align=justify>[[File:C-eqn3b.png|140px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
| + | <table width=400 align=center><td> | ||
| + | <p align=justify>[[File:C-eqn3c.png|140px|center]] | ||
| + | </p> | ||
| + | </td></table> | ||
Revision as of 08:06, 19 July 2011
Introduction
Light can be described as a periodic electromagnetic plane wave which carries energy in the form of an electromagnetic field. The electric and magnetic components can be written as:
This represents a monochromatic (single-frequency) beam travelling in the + z direction having a wavelength λ and frequency v (related by λ ν = c). The angle
is called the phase of the plane wave. A point on the wave having a constant phase (e.g. the peak of a sine wave) moves at a velocity determined by setting the time derivative of the constant phase equal to zero