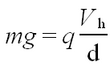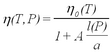Difference between revisions of "Main Page/PHYS 3220/Millikan"
(Created page with "<h1>Determination of the Electric Charge Unit: The Millikan Oil-Drop Experiment</h1> <h1>Abstract</h1> <p>In this experiment charged droplets of oil, in air, moving under gravit...") |
|||
| Line 19: | Line 19: | ||
<h1> Theory</h1> | <h1> Theory</h1> | ||
<p>A charge ''q'', situated in an electric field <b>E</b> experiences a force <b>F</b> = ''q'' <b>E</b>. If a potential difference ''V'' is applied to two parallel plates separated by a distance ''d'', the constant electric field between the plates is perpendicular to the plane defined by the plates and its magnitude is given as ''E''=''V''/''d''. Thus, by changing the voltage it is possible to counteract the gravitational acceleration ''g'' and hence to suspend a macroscopic particle of mass ''m'' with charge ''q'' according to</p> | <p>A charge ''q'', situated in an electric field <b>E</b> experiences a force <b>F</b> = ''q'' <b>E</b>. If a potential difference ''V'' is applied to two parallel plates separated by a distance ''d'', the constant electric field between the plates is perpendicular to the plane defined by the plates and its magnitude is given as ''E''=''V''/''d''. Thus, by changing the voltage it is possible to counteract the gravitational acceleration ''g'' and hence to suspend a macroscopic particle of mass ''m'' with charge ''q'' according to</p> | ||
| + | |||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn1.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(1)</b></td></tr></table> | ||
| + | <p>To determine ''q'' it is necessary to know ''m'', i.e., a measurement of the voltage that suspends the particle ''V<sub>h</sub>'' is not sufficient to find the value of ''q''. It is possible to find the mass m from a determination of the motion of the object without electric fields applied. However, it is necessary to take into account the viscosity of air at the given temperature and pressure thermometer and barometer (Digital). For gases (and fluids) a simple model of the viscous force is provided by Stokes' law. According to this law freely falling bodies reach a force equilibrium over a short distance with a terminal velocity ''v<sub>1</sub>''. For a spherical droplet of oil with radius ''a'' and a given viscosity ''η'' for the medium through which the droplet moves, the frictional force is given by</p> | ||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn2.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(2)</b></td></tr></table> | ||
| + | <p>Here we take into account the density of air ''σ'' as well as the density of oil ''ρ'' to determine the gravitational force (buoyancy) as</p> | ||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn3.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(3)</b></td></tr></table> | ||
| + | <p>Thus, a determination of the terminal velocity v1 that arises from the condition ''F<sub>S</sub>=F<sub>g</sub>'' allows us to find the radius of the droplet (and thus the mass). Since the radius of the droplet is relevant for a refined discussion of the viscous force, it is worthwhile to calculate it for each observed droplet from the terminal velocity v1 under gravity <b>(derive!)</b>:</p> | ||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn4.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(4)</b></td></tr></table> | ||
| + | <p>This estimate is based on the assumption of Stokes’ law, and, thus, in his later work Millikan has also used an expression that makes use of both terminal velocities (ref. 1). It requires a previous estimate of the electric charge unit ''e'', and is obtained from a division of the conditions of force equilibrium with and without an electric field <b>(derive!)</b>:</p> | ||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn5.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(5)</b></td></tr></table> | ||
| + | <p>Here ''v<sub>2</sub>'' is the magnitude of the velocity obtained for the condition when a voltage ''V'' is used to overcome gravity and make the droplet move towards the upper plate of the condenser. In the limit of ''v<sub>2</sub>'' = 0 (suspended droplet) an estimate of the droplet radius can be made from the holding voltage ''V<sub>h</sub>'' itself. While this procedure may seem unsatisfactory, since it depends on a knowledge of the charge value ''e'' (or a multiple thereof for a multipli-charged droplet, q=ne), a discrepancy between the determination of the charge radius from eqs. (4) and (5) points clearly to a problem with the knowledge of the viscosity for droplets of varying size.</p> | ||
| + | <p>A small m''odification of the force balance is required if an arbitrary voltage is applied. In Millikan's original setup only fixed voltages ''V could be obtained from a battery, and therefore, it was necessary to determine two terminal velocities: ''v<sub>1</sub>'' for ''V''=0, and ''v<sub>2</sub>''for the case where the voltage overcomes gravity. Derive the expressions required to calculate the charge of the droplet for both methods. The buoyancy of air is so small compared to the gravitational pull on the droplet that it can be neglected ( σ << ρ ).</p> | ||
| + | <p>The charge of the droplet when using method (I), i.e., finding ''V<sub>h</sub>'' and the 'free' terminal velocity ''v<sub>1</sub>'' is given as (using MKSA units, an approximation is given for quick lab calculations (use ''v<sub>1</sub>'' in m/s):</p> | ||
| + | |||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn6.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(6)</b></td></tr></table> | ||
| + | |||
| + | |||
| + | <p>For method (II) the charge is obtained from the expression</p> | ||
| + | |||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn7.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(7)</b></td></tr></table> | ||
| + | |||
| + | <p>A remaining problem concerns the applicability of Stokes' law for small droplets. Viscosity is caused by intermolecular forces in the medium (in our case the air). The Stokes law describes a macroscopic force that averages over the Brownian motion of molecules. Kinetic theory is capable of calculating values of viscosity for matter on the basis of modeling molecular collisions. The validity of the force law becomes questionable for particles whose size is comparable to the mean free path l of the air molecules. After several years of study Millikan reported the results of systematic investigations of oil drop charge measurements as a function of atmospheric pressure in the chamber (i.e., variation of ''l''). The correction of the viscosity is expressed in terms of the dimensionless parameter l/a as (ref. 2):</p> | ||
| + | |||
| + | |||
| + | <table width=200 align=center> | ||
| + | <tr><td> | ||
| + | <p align=justify>[[File:Mil-eqn8.png|110px|center]] | ||
| + | </p> | ||
| + | </td><td> <b>(8)</b></td></tr></table> | ||
| + | |||
| + | <p> | ||
Revision as of 09:38, 20 July 2011
Contents
Determination of the Electric Charge Unit: The Millikan Oil-Drop Experiment
Abstract
In this experiment charged droplets of oil, in air, moving under gravitational and electric fields are observed to verify the quantization of charge. The electric charge unit is determined to a few-percent accuracy. From the Brownian motion of the oil droplets one also obtains an estimate of Boltzmann’s constant.
Introduction
Millikan's determination of e, the charge of the electron (1909), proved that electric charges are quantized, i.e., occur as integer multiples of a unit. The measurement is performed on oil droplets that are ionized by the process of vaporization. To the present day it is true that for all elementary particles that can be freely observed, their electric charge is given as an integer multiple of a unit, i.e., q = n e. There exist, however, confined particles (quarks) that carry fractional charges of 1/3 and 2/3 of e.
The experiment makes use of an atomizer that generates oil droplets, some small fraction of which acquire positive or negative charges during the atomizing process. An electric condenser that can be charged to several hundreds of volts, and an illumination device as well as a telescope are included to observe the motion of the oil droplets. (Note that a radioactive source was used by Millikan to change the charge of droplets).
Under gravity the droplets move downwards. However, they are not in free-fall as a result of the viscosity of air, and the forces due to viscosity is described by Stokes' law. This frictional force results in a constant terminal velocity. Knowledge of the density and viscosity allows us to determine the mass of the droplet from the measured terminal velocity. The size of the droplet can be calculated by knowing the density of the oil.
Using an electric field of the right direction and magnitude Vh it is possible to counterbalance the gravitational force, i.e., to suspend the droplet (viscosity is irrelevant for a stationary droplet). This permits us to determine the charge of the droplet after the mass has been determined in the previous step.
An alternative method involves a measurement of the terminal velocity for a fixed voltage V that counteracts gravity. This was used by Millikan who did not have a continuously adjustable power supply to dial up the correct voltage for any given droplet, i.e. Vh. Both methods are used independently in this experiment.
A correction (due to Millikan) for the fact that the viscosity becomes smaller for droplets of a size comparable to the mean free path of air molecules has to be introduced for an accurate determination of the charge unit.
Theory
A charge q, situated in an electric field E experiences a force F = q E. If a potential difference V is applied to two parallel plates separated by a distance d, the constant electric field between the plates is perpendicular to the plane defined by the plates and its magnitude is given as E=V/d. Thus, by changing the voltage it is possible to counteract the gravitational acceleration g and hence to suspend a macroscopic particle of mass m with charge q according to
| (1) |
To determine q it is necessary to know m, i.e., a measurement of the voltage that suspends the particle Vh is not sufficient to find the value of q. It is possible to find the mass m from a determination of the motion of the object without electric fields applied. However, it is necessary to take into account the viscosity of air at the given temperature and pressure thermometer and barometer (Digital). For gases (and fluids) a simple model of the viscous force is provided by Stokes' law. According to this law freely falling bodies reach a force equilibrium over a short distance with a terminal velocity v1. For a spherical droplet of oil with radius a and a given viscosity η for the medium through which the droplet moves, the frictional force is given by
| (2) |
Here we take into account the density of air σ as well as the density of oil ρ to determine the gravitational force (buoyancy) as
| (3) |
Thus, a determination of the terminal velocity v1 that arises from the condition FS=Fg allows us to find the radius of the droplet (and thus the mass). Since the radius of the droplet is relevant for a refined discussion of the viscous force, it is worthwhile to calculate it for each observed droplet from the terminal velocity v1 under gravity (derive!):
| (4) |
This estimate is based on the assumption of Stokes’ law, and, thus, in his later work Millikan has also used an expression that makes use of both terminal velocities (ref. 1). It requires a previous estimate of the electric charge unit e, and is obtained from a division of the conditions of force equilibrium with and without an electric field (derive!):
| (5) |
Here v2 is the magnitude of the velocity obtained for the condition when a voltage V is used to overcome gravity and make the droplet move towards the upper plate of the condenser. In the limit of v2 = 0 (suspended droplet) an estimate of the droplet radius can be made from the holding voltage Vh itself. While this procedure may seem unsatisfactory, since it depends on a knowledge of the charge value e (or a multiple thereof for a multipli-charged droplet, q=ne), a discrepancy between the determination of the charge radius from eqs. (4) and (5) points clearly to a problem with the knowledge of the viscosity for droplets of varying size.
A small modification of the force balance is required if an arbitrary voltage is applied. In Millikan's original setup only fixed voltages V could be obtained from a battery, and therefore, it was necessary to determine two terminal velocities: v1 for V=0, and v2for the case where the voltage overcomes gravity. Derive the expressions required to calculate the charge of the droplet for both methods. The buoyancy of air is so small compared to the gravitational pull on the droplet that it can be neglected ( σ << ρ ).
The charge of the droplet when using method (I), i.e., finding Vh and the 'free' terminal velocity v1 is given as (using MKSA units, an approximation is given for quick lab calculations (use v1 in m/s):
| (6) |
For method (II) the charge is obtained from the expression
| (7) |
A remaining problem concerns the applicability of Stokes' law for small droplets. Viscosity is caused by intermolecular forces in the medium (in our case the air). The Stokes law describes a macroscopic force that averages over the Brownian motion of molecules. Kinetic theory is capable of calculating values of viscosity for matter on the basis of modeling molecular collisions. The validity of the force law becomes questionable for particles whose size is comparable to the mean free path l of the air molecules. After several years of study Millikan reported the results of systematic investigations of oil drop charge measurements as a function of atmospheric pressure in the chamber (i.e., variation of l). The correction of the viscosity is expressed in terms of the dimensionless parameter l/a as (ref. 2):
| (8) |