Main Page/PHYS 4210/Gamma Ray Spectroscopy

Gamma Ray Spectroscopy

In this experiment we study the gamma ray spectra of several radioactive elements to learn about the interaction properties of gamma rays with matter. The gamma rays are detected through ionization of the material in a scintillation counter, and the output pulse, which is generated with a photomultiplier tube, is then recorded with the aid of a Multi Channel Analyser (MCA) connected to a computer interface. The different types of interaction of gamma rays with matter are understood from a detailed analysis of the observed spectra. Thus, this experiment not only illustrates the physics of the interaction properties of photons, but also introduces scintillation detectors and relevant electronics.

Introduction

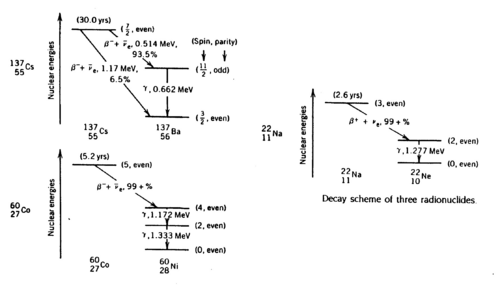
Gamma rays are photons of very short wavelength (~10^-12 cm) or very high frequency (10²² Hz) that are emitted during nuclear transitions. The decay schemes of the three radionuclides that we study (Na22, Cs137, Co60) are shown below. Read ref. 1-4 to get a clear idea of the significance of the gamma energies.

Figure 1 - Decay schemes of Cs-137, Co-60, and Na-22.

Method

Photons are electrically neutral, and unlike charged particles, do not experience the Coulomb force. They are, however, carriers of the electromagnetic force, and are able to ionize atoms through their interaction with matter, and this leads to the deposition of energy in the medium as the ionized particle slows down in traversing the medium. This energy can then be detected. The three modes of interaction are: photoelectric effect, Compton scattering, and pair production where the photon interacts with an atom, an electron, and a nucleus respectively. You should read the details of each type of interaction in the references and include this in your write-up. We summarise it briefly below.

Photoelectric effect

The photon of energy E_g is absorbed by an atom and an electron from one of the shells is emitted. If B_e is the binding energy of the electron, then the energy of the emitted electron will have an energy E_e = E_g - B_e. Since B_e is small (of the order 40 KeV) compared to E_g (of the order 1MeV), the electron carries most of the energy of the photon.

Compton scattering

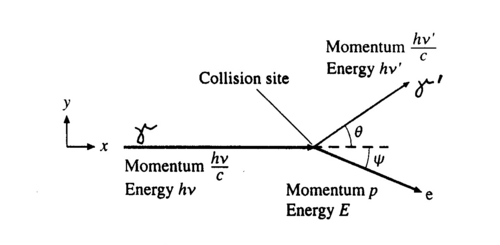
The photon scatters off an electron that is either free or is loosely bound in the atom, thereby scattering the electron. It can be shown (do so in your writeup) that the energy of the scattered electron is related to that of the incident photon, the angle of the scattered photon (theta), and the mass of the electron me through the relationship:

(1)

Figure 2 - Compton scattering.

Hence the scattered photon (of energy hv’) has the freedom to move at any angle with respect to the incident photon (or gamma ray, as we call it here), whereas the scattered electron is bound by the laws of conservation of momentum to only go in the forward direction. The kinetic energy of the Compton electron is E_C = hv- hv’. This, combined with the above formula for the energy of the electron shows that the maximum kinetic energy of the electron is when theta = 180° ,i.e., when the photon is scattered backwards. This maximum is known as the Compton edge.

Pair production

If the photon has more than twice the rest mass of an electron (0.511 MeV), the photon can produce an electron-positron pair. This must be done in the Coulomb field of the nucleus to balance linear momentum, as the photon cannot produce a pair in free space (its center of mass would have zero momentum). The energy in excess of the rest masses of the products is imparted as kinetic energy.

The energy dependencies of the three processes are quite different. At energies below a few KeV, the photoelectric effect dominates and the Coulomb effect is small, while pair production is energetically impossible. For the region of 0.1 to about 10 MeV, Compton scattering dominates. Above this, pair production is the predominant method for the interaction of the photons. It is important to realize that in photoelectric effect and pair production, the photon is eliminated in the process of the interaction, whereas in Compton scattering, the energy of the photon is only degraded. As explained further below the various processes involved lead to a complete or incomplete energy deposition of the gamma energy in the scintillator. We have to be concerned only with the first two methods; the photoelectric effect leads to complete energy deposition, while the Compton effect can lead to processes where the scattered gamma ray leaves the detector without depositing its energy.

The Radioactive Sources

You will be working with three radioactive sources: Na22, Cs 137, and Co60. You should note the radiation dosage marked on the source, and read about radiation safety and how to handle radiation sources from ref. 1, pg 326-328. Calculate the number of disintegrations per second for each of the sources based on the quoted dosage.

The Detector

The gamma rays that are emitted from the source are detected with a scintillator detector. In our laboratory, we use inorganic crystals of sodium iodide doped with impurity centres of thallium. This combination is denoted by NaI(Tl). A photon entering the detector ionizes the material through the processes described above. The positive ions and electrons created by the incoming photon diffuse through the lattice and are captured by the impurity centres i.e. the Tl atoms, which act as luminescence centres. Recombination produces an excited centre,which emits visible light upon its return to the ground state. The efficiency of these inorganic crystals is high, but the light output is spread over a time interval of the order of microseconds.

In general, for gamma rays less than 1 MeV, photons undergoing the photoelectric process will be completely absorbed and will give rise to a determined number of light quanta. These light quanta are then seen by the photomultiplier tube, and the output pulse will be proportional to the incoming energy of the gamma ray. The energy of the electrons produced by the Compton effect will depend on the angle at which they are scattered and hence there will be a spectrum of detected pulses. At energies above 1 MeV, pair production can occur and the electron and positron lose their kinetic energy by ionizing the medium. The electron is absorbed, while the positron annihilates within a few nanoseconds into two photons, each of 0.511 MeV. These may then interact through the photoelectric or Compton effect. There are three possibilities for the observed energy (show this in the writeup) depending on whether none, one or both of these photons from the positron annihilation are detected.

As mentioned, the produced light is proportional to the energy of the incident gamma ray. This light is then made incident on the photocathode face of a photomultiplier tube (PMT), which converts the photons to photoelectrons through the photoelectric effect. The electrons are amplified and then converted to a voltage pulse. The PMT used here has 10 stages and the multiplication for such tubes is about 10⁶ for an operational voltage between the cathode and the anode of 1000V. The cascade of electrons produced at each of the multiplication stages of the dynodes is collected at the anode, converted to a voltage pulse, which is then amplified and analysed. The PMT is enclosed in a high permeability material to shield against magnetic fields, as such effects would affect the efficiency of the tube.

Note that the metal shield that encloses the scintillator crystal does not allow β (or other charged) particles to permeate and deposit their usually well-defined energies. Thus, you should not expect to observe structures associated with, e.g., the 0.514 MeV and 1.17 MeV electrons coming from the Cs137 source with branching ratios of 93.5% and 6.5% respectively (cf.. Fig. 1). Charged particles are created inside the crystal by γ ray impact. There will be, however, backscattered γ rays from Compton scattering outside the crystal, e.g., off the backing of the source and off the lead shield.

Read the specifications for the model of the scintillator detector and photomultiplier that you have. Note that the size of the crystal is small. How does this affect your results? The typical quantum efficiency of scintillators of this type is one photon of light produced per 100 eV of energy deposited in the scintillator. The width of the full-energy peak (i.e. when the gamma energy is fully absorbed) depends on the number of light quanta produced by the incident gamma ray. The energy resolution, dE/E is an important quantity to consider as this factor will determine if we can separate gamma rays very close in energy.

The chain of events may help illustrate this point. The incident gamma ray of energy E_g produces a photoelectron with energy E_e ~ E_g. The photoelectron produces N light quanta in the scintillator material via ionization and excitation, each with an energy E_lq. Since the light is visible (~400 nm), E_lq is about 3 eV. This light falls on the photocathode, which has a quantum efficiency or sensitivity to the wavelength of the incident light. For the tube supplied, the efficiency peaks near 400 nm, making it quite suitable for use with a scintillator. Let

• ε(light) be the efficiency for the conversion of the excitation energy into light quanta
• ε(coll) be the efficiency for collecting the n lq light quanta at the photocathode of the PMT
• ε(cathode) be the efficiency for the cathode to eject a photoelectron