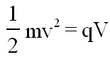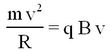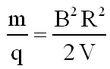Main Page/PHYS 4210/Mass Spectrometer

From Physics Wiki
Revision as of 12:27, 8 August 2011 by Junk (talk | contribs)
Jump to navigation Jump to search

Mass Spectrometer

The mass spectrometer is a device that separates and identifies ions according to their mass-to-charge ratio using the linear acceleration and deflection of ions, in electric and magnetic fields respectively.

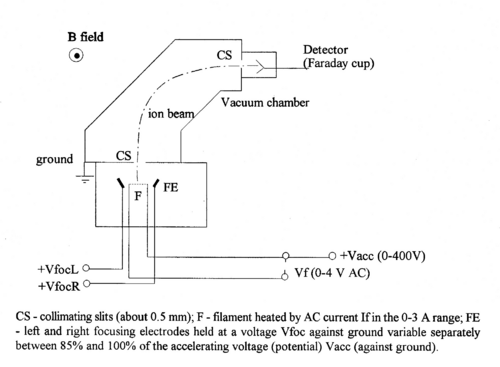
Mspec-fig1.png

Figure 1 - Schematic diagram of the magnetic selector mass spectrometer.

Key Concepts

  • Charge-to-mass ratio
  • A/D Converter
  • Mean free path
  • Faraday Cup
  • Diffusion pump
  • magnetic selector
  • Roughing pump
  • Ion gauge
  • Thermocouple gauge

Pre-Lab Requirement

This experiment has a prelab component. You must complete this exercise before you meet the TA for a demonstration.

Prepare a table of showing at which accelerating voltage you would expect to see a signal for the isotopes listed in the table below. Provide these for various values of magnetic field between 0.1T and 0.3T.

For example:

0.1 T0.12 T 0.14 T ...
1H
4He
6Li
7Li
...

Theory

A filament coated with a salt (e.g. sodium sulfate) when heated, produces neutral atoms and ions (e.g., Na+). This process of surface ionization works if the ionization potential of the atom is not too large compared to the work function of the metal (cf.. ref. 1).

In turn these ions are accelerated towards collimating slit by a potential difference V, and acquire a (small) kinetic energy of

Mspec-eqn1.png

 (1)

where q, m, and v are the charge, mass and velocity of the ions respectively.

Some ions pass through the collimating slit and into the homogeneous magnetic field of strength B, this field will deflect them into circular paths of radius R such that the centrifugal and magnetic forces balance. For this condition we have:

Mspec-eqn2.png

 (2)

Thence from eqs. 1 and 2 the mass-to-charge ratio is given by

Mspec-eqn3.png

 (3)

The value of R is fixed by the geometry of the spectrometer. In practice there is a problem with determining its accurate value, since the magnetic field has fringes both where the ions enter and exit. Therefore, it is not simply determined by the size of the magnet, but an effective radius has to be determined. By varying B or V, ions with different mass-charge ratios can be collected.

Assuming singly charged ions (q = 1e) and a radius that is fixed by the size of the magnet, we see that knowledge of V and B allows us to identify the mass of a given isotope.

  • e = 1.60 x 10-19 Coulombs
  • R = 4.8 x 10-2 meters (you may have to calibrate for a known mass number)
  • m = atomic weight in a.m.u., and 1 a.m.u. = 1.66 x 10-27 kg.

Note that the magnetic field strength B is measured in Tesla (in MKSA units). (The Earth's magnetic field has a strength on the order of 1 Gauss = 10-4 T). By reading the voltage at the peaks for a particular magnetic field, and substituting into equation (3), it is possible to identify the isotope(s) [use Maple or Mathematica].

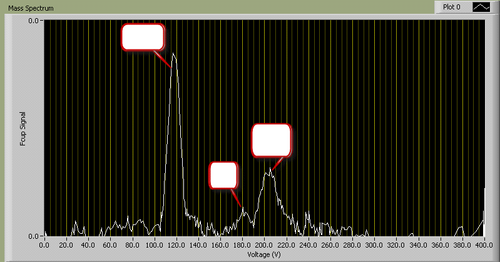
A typical I-V plot for fixed B looks as follows (identity of peaks removed):

Mspec-fig2.png

Figure 2 - A typical mass spectrum.

We provide a table with atomic weights for a few atoms that might appear in your spectrum. Consult a table of isotopes that can be found at the back of any Modern Physics text or in the CRC handbook.

Isotope Atomic Weight
1H 1.008
4He 4.004
6Li 6.017
7Li 7.018
7LiH 8.026
9Be 9.015
12C 12.004
14N 14.008
16O 16.000
23Na 22.990
24Mg 24.312
28Si 28.977
32S 31.972
39K 38.964
40Ca 39.363
41K 40.962
Retrieved from "https://physwiki.apps01.yorku.ca//index.php?title=Main_Page/PHYS_4210/Mass_Spectrometer&oldid=1169"