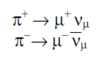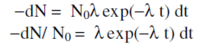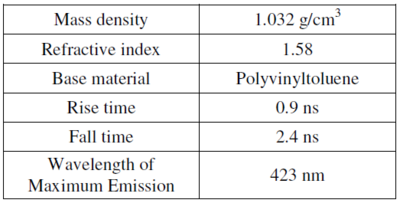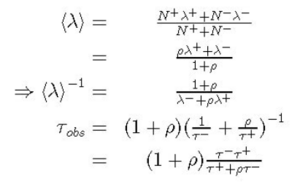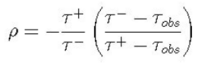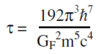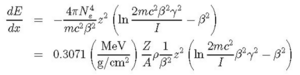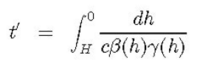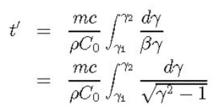Main Page/PHYS 4210/Muon Lifetime

Introduction

The muon is one of nature’s fundamental “building blocks of matter” and acts in many ways as if it were an unstable heavy electron, for reasons no one fully understands. Discovered in 1937 by C.W. Anderson and S.H. Neddermeyer when they exposed a cloud chamber to cosmic rays, its finite lifetime was first demonstrated in 1941 by F. Rasetti. The instrument described in this manual permits you to measure the charge averaged mean muon lifetime in plastic scintillator, to measure the relative flux of muons as a function of height above sea-level and to demonstrate the time dilation effect of special relativity. The instrument also provides a source of genuinely random numbers that can be used for experimental tests of standard probability distributions.

Our Muon Source

The top of earth's atmosphere is bombarded by a flux of high energy charged particles produced in other parts of the universe by mechanisms that are not yet fully understood. The composition of these "primary cosmic rays" is somewhat energy dependent but a useful approximation is that 98% of these particles are protons or heavier nuclei and 2% are electrons. Of the protons and nuclei, about 87% are protons, 12% helium nuclei and the balance are still heavier nuclei that are the end products of stellar nucleosynthesis.

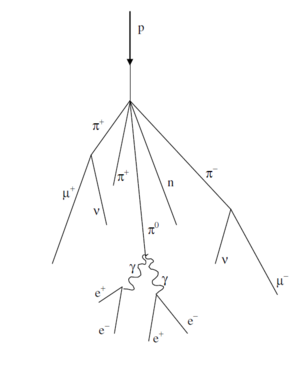
The primary cosmic rays collide with the nuclei of air molecules and produce a shower of particles that include protons, neutrons, pions (both charged and neutral), kaons, photons, electrons and positrons. These secondary particles then undergo electromagnetic and nuclear interactions to produce yet additional particles in a cascade process. Figure 1 indicates the general idea. Of particular interest is the fate of the charged pions produced in the cascade. Some of these will interact via the strong force with air molecule nuclei but others will spontaneously decay (indicated by the arrow) via the weak force into a muon plus a neutrino or antineutrino:

The muon does not interact with matter via the strong force but only through the weak and electromagnetic forces. It travels a relatively long instance while losing its kinetic energy and decays by the weak force into an electron plus a neutrino and antineutrino. We will detect the decays of some of the muons produced in the cascade. (Our detection

efficiency for the neutrinos and antineutrinos is utterly negligible.)

Figure 1- Cosmic ray cascade induced by a cosmic ray proton striking an air molecule nucleus.

Not all of the particles produced in the cascade in the upper atmosphere survive down to sea-level due to their interaction with atmospheric nuclei and their own spontaneous decay. The flux of sea-level muons is approximately 1 per minute per cm2 (see for more precise numbers) with a mean kinetic energy of about 4 GeV.

Careful study shows that the mean production height in the atmosphere of the muons detected at sea-level is approximately 15 km. Travelling at the speed of light, the transit time from production point to sea-level is then 50 μsec. Since the lifetime of at-rest muons is more than a factor of 20 smaller, the appearance of an appreciable sealevel muon flux is qualitative evidence for the time dilation effect of special relativity.

Muon Decay Time Distribution

The decay times for muons are easily described mathematically. Suppose at some time t we have N(t) muons. If the probability that a muon decays in some small time interval dt is λdt, where λ is a constant “decay rate” that characterizes how rapidly a muon decays, then the change dN in our population of muons is just dN = −N(t)λ dt, or dN/N(t) = −λdt. Integrating, we have N(t) = N₀exp(−λ t), where N(t) is the number of surviving muons at some time t and N₀ is the number of muons at t = 0. The "lifetime" t of a muon is the reciprocal of λ, t = 1/λ. This simple exponential relation is typical of radioactive decay.

Now, we do not have a single clump of muons whose surviving number we can easily measure. Instead, we detect muon decays from muons that enter our detector at essentially random times, typically one at a time. It is still the case that their decay time distribution has a simple exponential form of the type described above. By decay time distribution D(t), we mean that the time-dependent probability that a muon decays in the time interval between t and t + dt is given by D(t)dt. If we had started with N₀ muons, then the fraction −dN/N₀ that would on average decay in the time interval between t and t + dt is just given by differentiating the above relation:

The left-hand side of the last equation is nothing more than the decay probability we seek, so D(t) = l exp(−λ t). This is true regardless of the starting value of N₀. That is, the distribution of decay times, for new muons entering our detector, is also exponential with the very same exponent used to describe the surviving population of muons. Again, what

we call the muon lifetime is t = 1/λ.

Because the muon decay time is exponentially distributed, it does not matter that the muons whose decays we detect are not born in the detector but somewhere above us in the atmosphere. An exponential function always “looks the same” in the sense that whether you examine it at early times or late times, its e-folding time is the same.

Detector Physics

The active volume of the detector is a plastic scintillator in the shape of a right circular cylinder of 15 cm diameter and 12.5 cm height placed at the bottom of the black anodized aluminum alloy tube. Plastic scintillator is transparent organic material made by mixing together one or more fluors with a solid plastic solvent that has an aromatic ring structure. A charged particle passing through the scintillator will lose some of its kinetic energy by ionization and atomic excitation of the solvent molecules. Some of this deposited energy is then transferred to the fluor molecules whose electrons are then promoted to excited states. Upon radiative de-excitation, light in the blue and near-UV portion of the electromagnetic spectrum is emitted with a typical decay time of a few nanoseconds. A typical photon yield for a plastic scintillator is 1 optical photon emitted per 100 eV of deposited energy. The properties of the polyvinyltoluene-based scintillator used in the muon lifetime instrument are summarized in table 1.

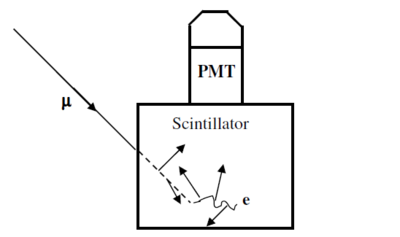
To measure the muon's lifetime, we are interested in only those muons that enter, slow, stop and then decay inside the plastic scintillator. Figure 2 summarizes this process. Such muons have a total energy of only about 160 MeV as they enter the tube. As a muon slows to a stop, the excited scintillator emits light that is detected by a photomultiplier tube (PMT), eventually producing a logic signal that triggers a timing clock. (See the electronics section below for more detail.) A stopped muon, after a bit, decays into an electron, a neutrino and an anti-neutrino. (See the next section for an important qualification of this statement.) Since the electron mass is so much smaller that the muon mass, m_μ/m_e ~ 210, the electron tends to be very energetic and to produce scintillator light essentially all along its pathlength. The neutrino and anti-neutrino also share some of the muon's total energy but they entirely escape detection. This second burst of scintillator light is also seen by the PMT and used to trigger the timing clock. The distribution of time intervals between successive clock triggers for a set of muon decays is the physically interesting quantity used to measure the muon lifetime.

Figure 2- Schematic showing the generation of the two light pulses (short arrows) used in determining the muon lifetime. One light pulse is from the slowing muon (dotted line) and the other is from its decay into an electron or positron (wavey line).

Table 1- General Scintillator Properties.

Interaction of μ⁻’s with matter

The muons whose lifetime we measure necessarily interact with matter. Negative muons that stop in the scintillator can bind to the scintillator's carbon and hydrogen nuclei in much the same way as electrons do. Since the muon is not an electron, the Pauli exclusion principle does not prevent it from occupying an atomic orbital already filled with electrons. Such bound negative muons can then interact with protons

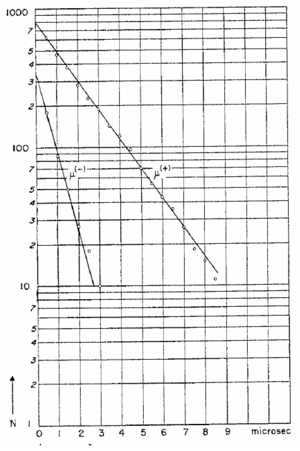
before they spontaneously decay. Since there are now two ways for a negative muon to disappear, the effective lifetime of negative muons in matter is somewhat less than the lifetime of positively charged muons, which do not have this second interaction mechanism. Experimental evidence for this effect is shown in figure 3 where “disintegration” curves for positive and negative muons in aluminum are shown . The abscissa is the time interval t between the arrival of a muon in the aluminum target and its decay. The ordinate, plotted logarithmically, is the number of muons greater than the corresponding abscissa. These curves have the same meaning as curves representing the survival population of radioactive substances. The slope of the curve is a measure of the effective lifetime of the decaying substance. The muon lifetime we measure with this instrument is an average over both charge species so the mean lifetime of the detected muons will be somewhat less than the free space value

t_μ = 2.19703 ± 0.00004 μsec.

The probability for nuclear absorption of a stopped negative muon by one of the scintillator nuclei is proportional to Z⁴, where Z is the atomic number of the nucleus . A stopped muon captured in an atomic orbital will make transitions down to the K-shell on a time scale short compared to its time for spontaneous decay . Its Bohr radius is roughly 200 times smaller than that for an electron due to its much larger mass, increasing its probability for being found in the nucleus. From our knowledge of hydrogenic wavefunctions, the probability density for the bound muon to be found inside the nucleus is proportional to Z³. Once inside the nucleus, a muon’s probability for encountering a proton is proportional to the number of protons there and so scales like Z. The net effect is for the overall absorption probability to scale like Z⁴. Again, this effect is relevant only for negatively charged muons.

Figure 3- Disintegration curves for positive and negative muons in aluminum. The ordinates at t = 0 can be used to determine the relative numbers of negative and positive muons that have undergone spontaneous decay. The slopes can be used to determine the decay time of each charge species.

μ⁺/μ⁻ Charge Ratio at Ground Level

Our measurement of the muon lifetime in plastic scintillator is an average over both negatively and positively charged muons. We have already seen that μ−’s have a lifetime somewhat smaller than positively charged muons because of weak interactions between negative muons and protons in the scintillator nuclei. This interaction probability is proportional to Z4, where Z is the atomic number of the nuclei, so the lifetime of negative muons in scintillator and carbon should be very nearly equal. This latter lifetime τ_c is measured to be τ_c = 2.043 ± 0.003 μsec..

It is easy to determine the expected average lifetime τ_obs of positive and negative muons in plastic scintillator. Let λ⁻ be the decay rate per negative muon in plastic scintillator and let λ⁺ be the corresponding quantity for positively charged muons. If we then let N^- and N⁺ represent the number of negative and positive muons incident on the scintillator per unit time, respectively, the average observed decay rate <λ> and its corresponding lifetime τ_obs are given by

where ρ ≡ N⁺/N⁻, τ⁻≡(λ⁻)⁻¹ is the lifetime of negative muons in scintillator and τ⁺≡(λ⁺)⁻¹ is the corresponding quantity for positive muons.

Due to the Z⁴ effect, τ⁻= τ_c for plastic scintillator, and we can set τ⁺ equal to the free space lifetime value τ_μ since positive muons are not captured by the scintillator nuclei. Setting ρ=1 allows us to estimate the average muon lifetime we expect to observe in the scintillator.

We can measure ρ for the momentum range of muons that stop in the scintillator by rearranging the above equation:

Backgrounds

The detector responds to any particle that produces enough scintillation light to trigger its readout electronics. These particles can be either charged, like electrons or muons, or neutral, like photons, that produce charged particles when they interact inside the scintillator. Now, the detector has no knowledge of whether a penetrating particle stops or not inside the scintillator and so has no way of distinguishing between light produced by muons that stop and decay inside the detector, from light produced by a pair of through-going muons that occur one right after the other. This important source of background events can be dealt with in two ways. First, we can restrict the time interval during which we look for the two successive flashes of scintillator light characteristic of muon decay events. Secondly, we can estimate the background level by looking at large times in the decay time histogram where we expect few events from genuine muon decay.

Fermi Coupling Constant G_F

Muons decay via the weak force and the Fermi coupling constant G_F is a measure of the strength of the weak force. To a good approximation, the relationship between the muon lifetime τ and G_F is particularly simple:

where m is the mass of the muon and the other symbols have their standard meanings. Measuring t with this instrument and then taking m from, say, the Particle Data Group produces a value for G_F.

Time Dilation Effect

A measurement of the muon stopping rate at two different altitudes can be used to demonstrate the time dilation effect of special relativity. Although the detector configuration is not optimal for demonstrating time dilation, a useful measurement can still be preformed without additional scintillators or lead absorbers. Due to the finite size of the detector, only muons with a typical total energy of about 160 MeV will stop inside the plastic scintillator. The stopping rate is measured from the total number of observed muon decays recorded by the instrument in some time interval. This rate in turn is proportional to the flux of muons with total energy of about 160 MeV and this flux decreases with diminishing altitude as the muons descend and decay in the atmosphere. After measuring the muon stopping rate at one altitude, predictions for the stopping rate at another altitude can be made with and without accounting for the time dilation effect of special relativity. A second measurement at the new altitude distinguishes between competing predictions.

A comparison of the muon stopping rate at two different altitudes should account for the muon’s energy loss as it descends into the atmosphere, variations with energy in the shape of the muon energy spectrum, and the varying zenith angles of the muons that stop in the detector. Since the detector stops only low energy muons, the stopped muons detected by the low altitude detector will, at the elevation of the higher altitude detector, necessarily have greater energy. This energy difference ΔE(h) will clearly depend on the pathlength between the two detector positions.

Vertically travelling muons at the position of the higher altitude detector that are ultimately detected by the lower detector have an energy larger than those stopped and detected by the upper detector by an amount equal to DE(h). If the shape of the muon energy spectrum changes significantly with energy, then the relative muon stopping rates at the two different altitudes will reflect this difference in spectrum shape at the two different energies. (This is easy to see if you suppose muons do not decay at all.) This variation in the spectrum shape can be corrected for by calibrating the detector in a manner described below.

Like all charged particles, a muon loses energy through coulombic interactions with the matter it traverses. The average energy loss rate in matter for singly charged particles traveling close to the speed of light is approximately 2 MeV/g/cm², where we measure the thickness s of the matter in units of g/cm². Here, s = ρx, where ρ is the mass density of the material through which the particle is passing, measured in g/cm³, and the x is the particle’s pathlength, measured in cm. (This way of measuring material thickness in units of g/cm² allows us to compare effective thicknesses of two materials that might have very different mass densities.) A more accurate value for energy loss can be determined from the Bethe-Bloch equation.

Here N is the number of electrons in the stopping medium per cm³, e is the electronic charge, z is the atomic number of the projectile, Z and A are the atomic number and weight, respectively, of the stopping medium. The velocity of the projectile is b in units of the speed c of light and its corresponding Lorentz factor is g. The symbol I denotes the mean excitation energy of the stopping medium atoms. Approximately, I=AZ, where A≈ 13 eV. More accurate values for I, as well as corrections to the Bethe-Bloch equation,

can be found here.

A simple estimate of the energy lost DE by a muon as it travels a vertical distance H is DE = 2 MeV/g/cm² * H * ρ_air, where ρ_air is the density of air, possibly averaged over H using the density of air according to the “standard atmosphere.” Here the atmosphere is assumed isothermal and the air pressure p at some height h above sea level is parameterized by p = p₀ exp(-h/h₀), where p₀ = 1030 g/cm² is the total thickness of the atmosphere and h₀ = 8.4 km. The units of pressure may seem unusual to you but they are completely acceptable. From hydrostatics, you will recall that the pressure P at the base of a stationary fluid is P = ρgh. Dividing both sides by g yields P/g = ρh, and you will then recognize the units of the right hand side as g/cm². The air density r, in familiar units of g/cm³, is given by ρ = −dp/dh.

If the transit time for a particle to travel vertically from some height H down to sea level, all measured in the lab frame, is denoted by t, then the corresponding time in the particle’s rest frame is t’ and given by

Here β and γ have their usual relativistic meanings for the projectile and are measured in the lab frame. Since relativistic muons lose energy at essentially a constant rate when travelling through a medium of mass density ρ, dE/ds = C0, so we have dE = ρC₀ dh, with C₀ = 2 MeV/(g/cm2). Also, from the Einstein relation, E = γmc², dE = mc² dγ, so dh = (mc²/ρC₀) dγ. Hence,

Here γ₁ is the muon’s gamma factor at height H and γ₂ is its gamma factor just before it enters the scintillator. We can take γ₂ = 1.5 since we want muons that stop in the scintillator and assume that on average stopped muons travel halfway into the scintillator, corresponding to a distance s = 10 g/cm². The entrance muon momentum is then taken from range-momentum graphs at the Particle Data Group WWW site and the corresponding γ₂ computed. The lower limit of integration is given by γ₁ = E1/mc², where

E₁ = E₂ + ΔE, with E₂ =160 MeV. The integral can be evaluated numerically. (See, for example, )

Hence, the ratio R of muon stopping rates for the same detector at two different positions separated by a vertical distance H, and ignoring for the moment any variations in the shape of the energy spectrum of muons, is just R = exp(− t’/τ ), where τ is the muon proper lifetime.

When comparing the muon stopping rates for the detector at two different elevations, we must remember that muons that stop in the lower detector have, at the position of the upper detector, a larger energy. If, say, the relative muon abundance grows dramatically with energy, then we would expect a relatively large stopping rate at the lower detector simply because the starting flux at the position of the upper detector was so large, and not because of any relativistic effects. Indeed, the muon momentum spectrum does peak, at around p = 500 MeV/c or so, although the precise shape is not known with high accuracy. See figure 4.

Figure 4- Muon momentum spectrum at sea level. The curves are fits to various data sets (shown as geometric shapes).

We therefore need a way to correct for variations in the shape of the muon energy spectrum in the region from about 160 MeV – 800 MeV. (Corresponding to momentums’s p = 120 MeV/c – 790 MeV/c.) We do this by first measuring the muon stopping rate at two different elevations (Δh = 3008 meters between Taos, NM and Dallas, TX) and then computing the ratio R_raw of raw stopping rates. (R_raw = Dallas/Taos = 0.41 ± 0.05) Next, using the above expression for the transit time between the two elevations, we compute the transit time in the muon’s rest frame (t’ = 1.32τ) for vertically travelling muons and calculate the corresponding theoretical stopping rate ratio R = exp(− t’/τ ) = 0.267. We then compute the double ratio R0 = R_raw /R = 1.5 ± 0.2 of the measured stopping rate ratio to this theoretical rate ratio and interpret this as a correction factor to account for the increase in muon flux between about E =160 MeV and E = 600 MeV. This correction is to be used in all subsequent measurements for any pair of elevations.

To verify that the correction scheme works, we take a new stopping rate measurement at a different elevation (h = 2133 meters a.s.l. at Los Alamos, NM), and compare a new stopping rate ratio measurement with our new, corrected theoretical prediction for the stopping rate ratio R_μ = R₀ R = 1.6exp(− t’/τ). We find t’ = 1.06τ and R_μ = 0.52 ± 0.06. The raw measurements yield R_raw = 0.56 ± 0.01, showing good agreement.

For your own time dilation experiment, you could first measure the raw muon stopping rate at an upper and lower elevation. Accounting for energy loss between the two elevations, you first calculate the transit time t’ in the muon’s rest frame and then a naïve theoretical lower elevation stopping rate. This naïve rate should then be multiplied by the muon spectrum correction factor 1.5 ± 0.2 before comparing it to the measured rate at the lower elevation. Alternatively, you could measure the lower elevation stopping rate, divide by the correction factor, and then account for energy loss before predicting what the upper elevation stopping rate should be. You would then compare your prediction against a measurement.

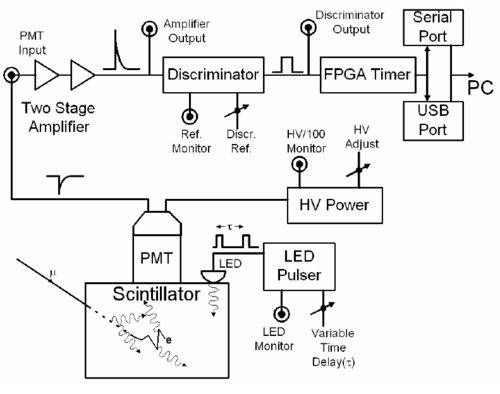
Electronics

A block diagram of the readout electronics is shown in figure 5. The logic of the signal processing is simple. Scintillation light is detected by a photomultiplier tube (PMT) whose output signal feeds a two-stage amplifier. The amplifier output then feeds a voltage comparator (“discriminator”) with adjustable threshold. This discriminator produces a TTL output pulse for input signals above threshold and this TTL output pulse triggers the timing circuit of the FPGA. A second TTL output pulse arriving at the FPGA input within a fixed time interval will then stop and reset the timing circuit. (The reset takes about 1 msec during which the detector is disabled.) The time interval between the start and stop timing pulses is the data sent to the PC via the communications module that is used to determine the muon lifetime. If a second TTL pulse does not arrive within the fixed time interval, the timing circuit is reset automatically for the next measurement.

Figure 5- Block diagram of the readout electronics. The amplifier and discriminator outputs are available on the front panel of the electronics box. The HV supply is inside the detector tube.

The front panel of the electronics box is shown in figure 6. The amplifier output is accessible via the BNC connector labeled Amplifier output. Similarly, the comparator output is accessible via the connector labeled Discriminator output. The voltage level against which the amplifier output is compared to determine whether the comparator triggers can be adjusted using the “Threshold control” knob. The threshold voltage is monitored by using the red and black connectors that accept standard multimeter probe leads. The toggle switch controls a beeper that sounds when an amplifier signal is above the discriminator threshold. The beeper can be turned off.

Figure 6- Front of the electronics box.

The back panel of the electronics box is shown is figure 7. An extra fuse is stored inside the power switch.

Figure 7- Rear of electronics box. The communications ports are on the left. Use only one.

Figure 8 shows the top of the detector cylinder. DC power to the electronics inside the detector tube is supplied from the electronics box through the connector DC Power. The high voltage (HV) to the PMT can be adjusted by turning the potentiometer located at the top of the detector tube. The HV level can be measured by using the pair of red and black connectors that accept standard multimeter probes. The HV monitor output is 1/100 times the HV applied to the PMT.

Figure 8- Top view of the detector lid. The HV adjustment potentiometer and monitoring ports for the PMT are located here.

A pulser inside the detector tube can drive a light emitting diode (LED) imbedded in the scintillator. It is turned on by the toggle switch at the tube top. The pulser produces pulse pairs at a fixed repetition rate of 100 Hz while the time between the two pulses comprising a pair is adjusted by the knob labeled Time Adj. The pulser output voltage is accessible at the connector labeled Pulse Output.

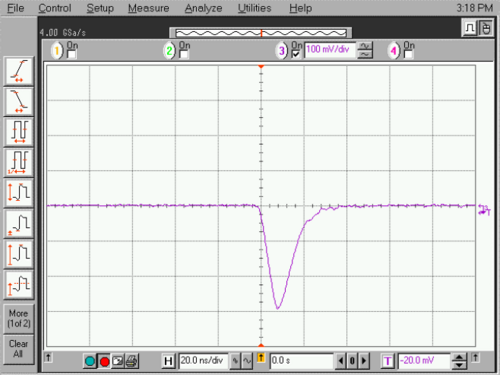
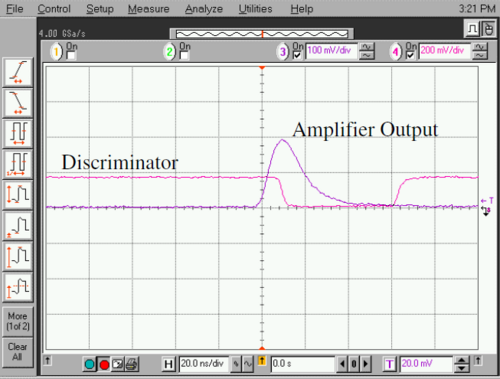
For reference, Figure 9 shows the output directly from the PMT into a 50Ω load. Figure 10 shows the corresponding amplifier and discriminator output pulses.

Figure 9- Output pulse directly from PMT into a 50Ω load. Horizontal scale is 20 ns/div and vertical scale is 100 mV/div.

Figure 10- Amplifier output pulse from the input signal from figure 9 and the resulting discriminator output pulse. Horizontal scale is 20 ns/div and the vertical scale is 100 mV/div (amplifier output) and 200 mV/div (discriminator output).