Main Page/PHYS 3220/Digital Oscilloscope

Digital Storage Oscilloscope

In this experiment we use a clock pulse generator to produce rectangular pulses which are recorded and analyzed using a modern digital storage oscilloscope capable of performing a fast fourier transform (FFT) on a given signal. Then the behaviour of a simple RC (integrator) circuit fed by a square wave pulse is analyzed both in the steady-state and transient (turn-on) regimes. Finally the square-wave pulse is used to induce damped harmonic motion in an LC circuit.

Introduction

The behaviour of short time-varying signals can be investigated easily with a digital storage oscilloscope (DSO) that will allow you to trigger single events and to store them for any length of time. Periodic signals play an important role in many areas of physics. Periodic signals are conveniently analyzed in terms of harmonic (or frequency) content, either by means of a Fourier series or by a Fourier transform [1]. Typically, oscilloscopes display signals in the time domain. The DSO you are using here will allow you to process these signals so they can be displayed in the frequency domain by using an FFT signal processing module included in the DSO. For a finite wavetrain recorded at discrete time intervals two parameters impose practical limitations on acquiring knowledge about the frequency content of a pulse. The sampling rate Δt limits the maximum frequency that can be recorded (intuitively: a signal that changes sign at every t_j = j Δt has the highest frequency that can be represented on the discrete time axis). The length of the recorded signal T limits the frequency resolution Δf: the lowest frequency that can be recorded corresponds to a wave with a period that equals T.

Thus, the Fourier transform that would be available in an ideal measurement (continuous sampling and infinite length of measurement)

(1)

this is replaced by a discrete Fourier transform:

(2)

where the length of the signal in the time domain is given by T = N Δt , the maximum frequency (called the Nyquist frequency) is actually one-half of the inverse sampling rate f_c = 1/(2 Δt) as the range of frequencies ranges in principle from -f_c to f_c (but the answer is symmetric in f so we are only interested in the range [0, f_c]). The frequency resolution equals Δf = 1/(N Δt). There are numerous problems associated with the replacement of eq (1) by eq (2), these problems are discussed in detail in [2] (and hinted at in the manual for the Tektronix DS210 oscilloscope). To minimize some of the errors one usually multiplies the time signal with a window function whose main purpose is to provide a smooth switching of the pulse and thereby to eliminate artificial high-frequency components that would be associated with chopping a periodic signal at t = 0 and t = T and assuming periodicity (wrap-around).

In a digital storage oscilloscope (as in computer programs that analyze recorded data) an FT function is provided by an efficient algorithm (fast FT = FFT) [2]. In a computer interfaced experiment one usually chooses the sampling rate and temporal record length freely. However, with the DSO these parameters are not independent and are actually controlled simultaneously by the DSO time base control. Furthermore, the number of points used in memory (for display on the screen and transfer to a computer) for a single trace is fixed. The FFT algorithm requires this number to be a power of 2 (typical numbers are 1024, 2048, etc. ).

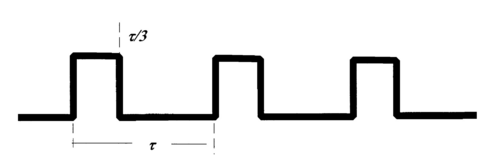
Consider a rectangular pulse, and a square-wave in particular. It can be thought of as a superposition of a sine wave with the same period τ, given by admixtures of sine waves with higher frequencies (or periods that are simple fractions of τ). This is known from Fourier series expansions of this periodic function. Only sine waves with odd multiples of the base frequency contribute (odd-order harmonics), and the coefficients in the linear combination can be calculated [1]. In part 1 of the experiment the Fourier spectrum (which could detect any frequency components, and not just multiples of the base frequency) is taken for rectangular pulses with different duty cycles. The objective is to show that for a pulse with duty cycle (τ/n)/τ = 1:n (cf.. Fig. 1) the n^th harmonic is absent. For a square-wave pulse (1:2) only odd orders appear.

Figure 1 - A rectangular pulse with a duty cycle of 1:3.

For a square wave pulse the harmonic coefficients can be calculated from the Fourier series expansion to be (we assume a signal that ranges between 0 and 1)

(3)

Procedure

Part 1: Harmonic Analysis of Rectangular Pulses

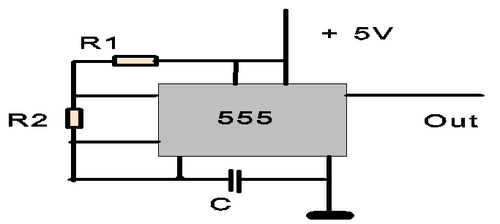
Consider the circuit diagram for a clock pulse generator built around a special-purpose integrated timer circuit. (The 555 timer from any electronic supplier. The 555 timer date sheet .pdf format can be downloaded for free from many sources on the internet; just search for “555 timer.”). The variable timing of the on- and off duty cycles is provided by two resistors and a capacitor (two time constants of type τ = RC).

Figure 1 - Circuit diagram for timer based on 555 IC.

The details of the timer IC are explained in ref. [3]. The capacitor C will charge through (R₁+R₂), yet discharge only through R₂.Therefore, R₁ and R₂ do not simply control (together with C) the duration of the high and low states respectively. The switching behaviour of the timer IC depends on the inputs of the gates to which the resistors are connected with respect to the comparators the voltage levels at the respective trip points will be 1/3 and 2/3 of the operating voltage. The period of the signal is independent of the operating voltage and can be estimated to be T=0.693(R₁+2R₂)C.

The Tektronix TDS210 Oscilloscope

Familiarize yourself with the effect of varying the two resistors, and learn how to use the digital scope. There are several menus that control the scope operation. For this part you need to use the menu that controls the first Y channel (CH 1), and possibly the TRIGGER menu. In the TRIGGER menu it is important that the Source of triggering be specified as CH 1 and the Mode of triggering be set on Auto. (Only for the measurement of the transient behaviour of an RC circuit will you need to switch to Single Mode). The 5 buttons to the right of the LCD display are used to toggle through the options indicated on the DSO screen.