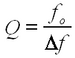Main Page/PHYS 4210/Johnson Noise
Johnson Noise
In this experiment we use an instrumentation amplifier, bandpass filter, and amplitude detector to investigate the noise generated by thermal fluctuations in a resistor, called Johnson noise. Various characteristics of this noise are investigated such as the dependence of the RMS noise voltage on the resistor value, on the bandwidth selected by the filter, and also on temperature.
Introduction
Thermal fluctuations are usually investigated in the context of the Brownian motion of molecules (e.g., in the Millikan oil drop experiment), but they permeate other branches of physics. In this experiment we investigate the manifestations of thermal energy fluctuations at room temperature (energy kT, where k is the Boltzmann constant) in a solid, which can be a resistor made of metal wire or a made of a metal film [1]. It will be demonstrated that the energy available due to kT (on average) are responsible for voltage fluctuations across the resistor. Any resistor in an electronic circuit should be treated not only as a passive element which provides a voltage drop for a current passing through it according to Ohm’s law, but, in fact, also as a generator of so-called white noise. Thus, the present experiment not only serves to demonstrate the wonders of physics at non-zero temperature, but also demonstrates the practical importance: noise is unavoidable, one has to make efforts to minimize its effect.
The term white noise refers to the frequency characteristic: in principle, such noise has equal amplitude at all frequencies. In practice, there is a cut-off at high frequencies: when the frequencies f are so high that the quantum energy E = hf becomes comparable to the average thermal energy kT the classical approximation breaks down, and the spectral power density decreases, instead of remaining constant. This resolves the problem of an infinite total power which one would obtain, if the constant power density was integrated over all frequencies to infinity. At the frequencies considered in this laboratory, however, the spectral density is constant (calculate the critical frequency where quantum effects will kick in).
Nyquist [2] provided a consistent explanation for resistor noise. Derivations are offered in Statistical and Thermal Physics textbooks [3]. The root mean square (RMS) noise voltage is given as
| (1) |
Here R is the resistance, and Δf the bandwidth of the noise which has to be defined in some way, as the noise signal is usually measured over a finite frequency range, which usually, however, is not described by a simple square profile (minimum and maximum frequency). One can use for the bandwidth definition the points where the other wise flat transmission curve (ratio of output to input voltage) falls by 3 dB (understand what that means).
Johnson noise is not associated with the flow of current through the device. Other types of noise are:
- shot noise (e.g., in semiconductor devices and vacuum tubes, cf.. separate experiment), which is also white, and depends on the magnitude of the current, and is a manifestation of the quantization of charge;
- flicker noise or 1/f noise, which is an incompletely understood phenomenon common to amplifiers, and which includes low-frequency drifts that plague DC measurements in particular;
- interference noise, such as 60-cycle AC noise and its harmonics, radio frequency noise provided by radio stations, cell phones, etc. , cosmic radiation, transients associated with equipment being turned on or off, to name a few [4].
Life can be complicated for experimentalists!
For the experimental verification of this law one uses the following electronic modules:
- a pre-amplifier with high gain, and low intrinsic noise
- an amplifying (active) bandpass filter of variable bandwidth Δf, which is related to the quality factor according to (f0 is the centre frequency)
(2) - a full-wave precision rectifier, which turns an AC signal into a positive signal (possibly with additional selectable gain)
- a low-pass filter to integrate the rectified signal and thereby measure the RMS voltage.
These modules are contained in the TeachSpin Signal Processor/Lock-in Amplifier [5]. Figure 1 shows the front panel of the apparatus.
One of the functions of this experiment is to prepare you for the more sophisticated lock-in amplifier experiment. In parts 1-4 of the procedure you are asked to measure the characteristics of some of the modules. You will also use an oscilloscope to monitor the signals. It is possible with the high gain settings on the amplifier stages to oversaturate the signal (it will be clipped at about +/- 10 V), and only a careful monitoring of the signal at intermediate stages with an oscilloscope can prevent that from happening.
|
|