Main Page/PHYS 3220/Rutherford I

Introduction

The Rutherford scattering experiment, where alpha particles (doubly charged Helium nuclei) were scattered off of a target (gold, aluminum, etc.) represents one of the most important experiments of this century. While the bulk of the alpha particles were scattered at small angles, indicating a soft collision process, a finite number of alpha particles however did scatter at very large angles. This could only have occurred though a collision with a massive object. From the distance of closest approach of the alpha with this object, and using information on the size of the whole atom, we came to know that the atom was mostly empty space. The results of this experiment formed the basis of subatomic structure, as we know it today – that the atom has a hard central core consisting of a tiny but massive core called the nucleus, surrounded by electrons, forming an electrically neutral system.

In this experiment we reproduce the results of Rutherfordby allowing alpha particles from a radioactive source (Am-241) to impinge on thin gold foil. We then compare the experimentally observed differential cross section (related to the number of detected alpha particles), as a function of the angle of scatter of the alpha particles off the target atoms. By comparing these particles to the theoretical expectations of elastic scattering of two particles, we can confirm that the alpha predominantly scatter off the nuclear core of the atom, and hence the structure of the atom is as Rutherford suggested.

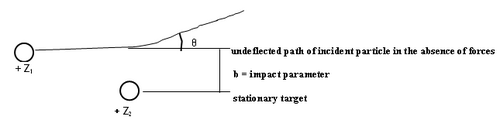
Theory

Figure 1 -

The theoretical analysis of the scattering cross section can be based on classical or quantum mechanics. In classical mechanics the number of particles scattered at a certain angle (θ) is a unique function of the impact parameter (b). We assume that a pure Coulomb potential is valid, but the appropriateness of this assumption shall be discussed later. To obtain the scattering cross section classically, first one solves Newton's equation of motion to obtain the relationship between impact parameter and scattering angle, and the results is that b 1/θ. Small impact parameters thus lead to close encounters of the two charged objects, and thus large scattering angles. Conversely, distant collisions lead to small scattering angles. In quantum mechanics this relationship is not unique, but interestingly, a probability distribution arises for the particles to reach deflection angles θ that are synonymous with the classical answer (this is a special feature of the Coulomb potential). Although this relation tells us we are on the right track intuitively, unfortunately it is not very useful since we cannot measure b in any given interaction. We have to relate the scattered angle to something we can measure: the number of alpha particles scattered into the solid angle of the detecting device.