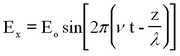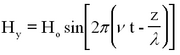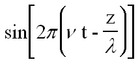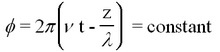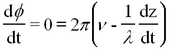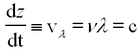Main Page/PHYS 3220/Speed of Light

<title>Hello </title>

Introduction

Light can be described as a periodic electromagnetic plane wave which carries energy in the form of an electromagnetic field. The electric and magnetic components can be written as:

This represents a monochromatic (single-frequency) beam travelling in the + z direction having a wavelength λ and frequency v (related by λ ν = c). The angle

is called the phase of the plane wave. A point on the wave having a constant phase (e.g. the peak of a sine wave) moves at a velocity determined by setting the time derivative of the constant phase equal to zero

The latter quantity v_λ is called the phase velocity of the plane wave. From the above we find that in vacuum the phase velocity of monochromatic light is frequency (colour) independent. This quantity is known to high precision and is called the velocity of light c. We will determine the value of c in this experiment.

This experiment uses pulses of light reflected from a spinning mirror, and thus a band of frequencies is present centered around the fundamental optical frequency. An accurate analysis requires the concept of a group velocity. Due to the length of the pulses we may treat the light as monochromatic in our experiment, and thus do not need to distinguish between group and phase velocities.

Method

Many methods for the determination of the speed of light have been developed. Since c = Δs / Δt is large, i.e. ~3 x 10⁸ m/sec., its measurement in the laboratory necessitates the measurements of small time increments Δt, for modest values of Δs. One may employ large path lengths of celestial dimensions to increase Δt to a value which may be recorded more accurately. This latter method was used in 1675 by Roemer (Δs = 1.86 x 10⁸ miles (the diameter of the Earth's orbit) gives Δt = 1000 sec). One can also perform the timing of the passage of light from its source to a distant mirror and then back to the source.

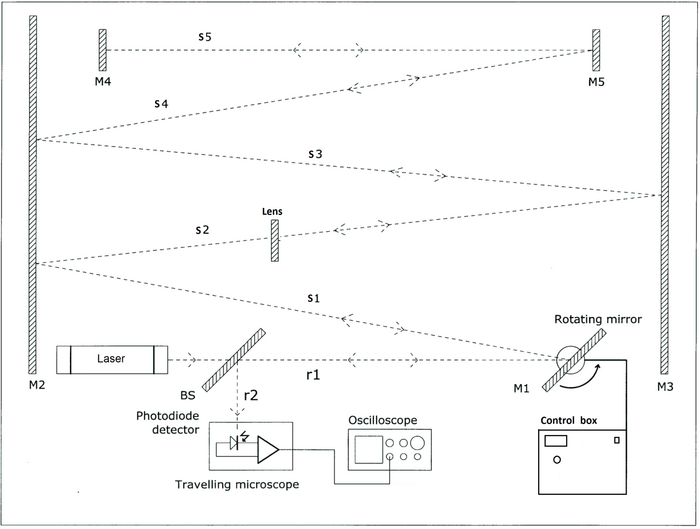
The rotating mirror method of Foucault, and later Michelson, provides a compromise between these two approaches. In this experiment (Fig. 1), a beam of light from a laser is reflected from a rotating mirror (M1) along a measured path by way of a series of secondary mirrors (M2, M3, M4, M5), which reflect it back along the original path to the rotating mirror. While the light pulse has been travelling along this path, the mirror has rotated slightly so that the returning light pulse reflected from the new position of the mirror will be deviated a small distance Δx from its original path. Relating the resulting deflection of the returning beam to the time taken for the mirror to rotate, and thus to the known path length, c is determined.

Referring to Fig. 1, the distance travelled by the light pulse is

(1)

The measured displacement of the returning pulse from its original position is

(2)

where α is the mirror’s rotation angle expressed in radians. Fig. 2

The time required for the mirror to rotate through this angle is

where ω = angular frequency of mirror = 2πf. Thus

(3)

hence combining equations 1 and 2, we have

(4)

Figure 1 - Experiment setup.

Procedure

CAUTION: Laser light is dangerous. Do not look directly into the beam. Understand the beam path of the laser source before switching the laser on.

Set up the apparatus as shown in Fig. 1 (check if it has been already aligned for you!). The beam from the laser travels a long path to the fixed mirror and back again, reflecting in both directions from the rotating mirror. It finally reflects from a partially reflecting mirror B5 and is focused by a short focal-length lens onto the scale. The spot size D and the angular divergence of the laser beam, θ (radians) are related by D = f θ, where f is the focal length. The rotation frequency of the mirror is controlled by a potentiometer (Variac).

The laser beam must be optically aligned at a slight upward angle with respect to all the other components. Once a component is aligned, do not disturb it, even slightly, or the entire process may have to be repeated! This can amount to a few hours of your time.

Aim the laser so that it strikes the stationary rotating-mirror (M1). Unplug the Variac. With the key, turn mirror (M1) until the beam is reflected back and just above the beam origin. Adjust either the actual position or the levelling screws as necessary. Then turn the key until mirror (M1) reflects the beam onto the first ¼ position of mirror (M2). Go to mirror (M2) and adjust it until the beam is reflected back onto mirror (M1). NEVER ADJUST THE EXISTING VERTICAL POSITION OF ANY ELEMENT IN THIS APPARATUS EXCEPT FOR M4 AND/OR M5. Next insert and centre the lens. Adjust until only one spot is observable at either mirror (M1) or mirror (M2) with no secondary beam images (check surrounding wall). M1 is also adjusted to center the reflected beam on mirror (M3). Repeat these steps until the beam strikes mirror (M5). This mirror can be adjusted to bring a reflected beam on center with mirror (M4). You will need to adjust both mirrors until the beam retraces its path, that is, with no secondary images. Finally, insert and align the half-silvered plate at 45o with equal distances to the laser and graph scale. Can you think of a procedure to optimise this step? Hint: think in terms of any secondary images. Do not in any way disturb the tables or you will have to begin again.

Part A

TEST RUN – Students verify their understanding of system.

An initial, rough method for approximating the speed of light is outlined below. A mounted graph-paper is used to measure x.

**Make sure the key is removed from the rotating-mirror before the power on the Variac is turned on.**

1. Determine the frequency of the rotating mirror. To give a good angular displacement to the light beam, the mirror should be rotating at about 400 c.p.s. (= 24,000 rpm).

   A tuning fork (of known frequency) is used to determine the rotation frequency of the motor. Accelerate the motor (making sure that the key is not in the top of the mirror when the motor is turned on) by turning the dial on the Variac. For a frequency of 400 cps, the voltage required will be about 100 V. Do not raise the voltage above 110 volts, and do not apply the voltage too quickly as you may burn the motor out.

   At this recorded frequency of rotation of mirror (1), mark the location on the graph paper scale of the laser beam. Next turn off the Variac (potentiometer) voltage. Using the key, adjust the mirror (1) until the beam again follows the original aligned path. This is easily noted in the dark, when the spot striking mirror (2) reflects directly back onto mirror (1). The position measurements of the image during rotation should be shifted a little distance, x, from the stationary aligned position. Substitute this x, the frequency f, and the component distances into the equation for c, the velocity of light. Include a discussion of the errors involved in this set-up. How could this set-up yield more accurate results?

Part B

The method and measuring equipment are now modified to allow an improved estimate of c.

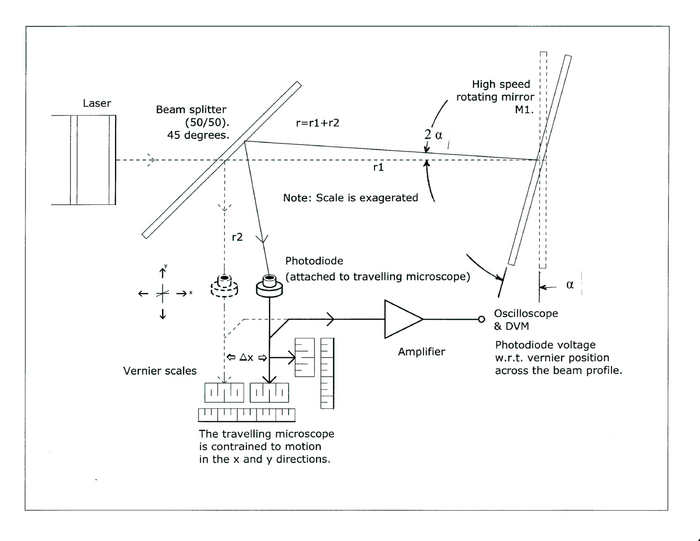
1. Replace the graph paper with a photodiode detector, mounted on a leveled travelling microscope, as shown in Fig 2. Note that the oscilloscope measurements rely on an accurate calibration of the “sweep” speed of the electron beam. The oscilloscope measures both the pulse amplitude and rotation frequency directly. The travelling microscope allows both horizontal and vertical measurements of image movement.
2. 2. At a number of frequencies, record the pulse-amplitude distributions, both horizontal and vertical. From this, determine the position of the pulse maxima. Graph these x values as a function of frequency. Include an error analysis in your report. Your least squares analysis should give a value and precision estimate of x. Is the least squares fit a satisfactory method? Measure exactly the position of the optical components. Substitute these values to determine c. Why do you see a spot image? (Why is it not a line image?)

Figure 2 - Use of a photodetector to determine pulse amplitude and period directly.

You have to keep in mind the following when performing the measurements and analysing your data: the displacement that you record for the photodetector at maximum amplitude has a significant error, since the maximum is flat (the laser spot is fuzzy due to vibrations in the rotating mirror). Investigate how your error estimate improves as the number of data points taken increases. Derive an error estimate for your speed of light measurement, and comment about whether the agreement with the literature value improves as you increase the number of data points (e.g., from three to six different Variac settings, i.e., rotation frequencies). Should you use the origin (location of the spot when the mirror is stationary) to obtain an absolute scale for the displacements or not? If yes, then you could constrain the fit to go through the origin.